Solution Sets

Algebra Level pending

What is the solution set of the following? x 2 + y 2 − 4 x + 6 y ≤ 3 x^{2}+y^{2}-4x+6y\leq3 and x 2 − y 2 − 4 x + 6 y ≤ 3 x^{2}-y^{2}-4x+6y\leq3 .

x x : x x ∈ ( x 2 + y 2 − 4 x + 6 y ≤ 3 \in(x^{2}+y^{2}-4x+6y\leq3 ) The solution set is all real numbers The solution is the empty set x x : x x ∈ ( x 2 − y 2 − 4 x + 6 y ≤ 3 \in(x^{2}-y^{2}-4x+6y\leq3 )

Hana Wehbi by Hana Wehbi , 51, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Hana Wehbi
May 26, 2016

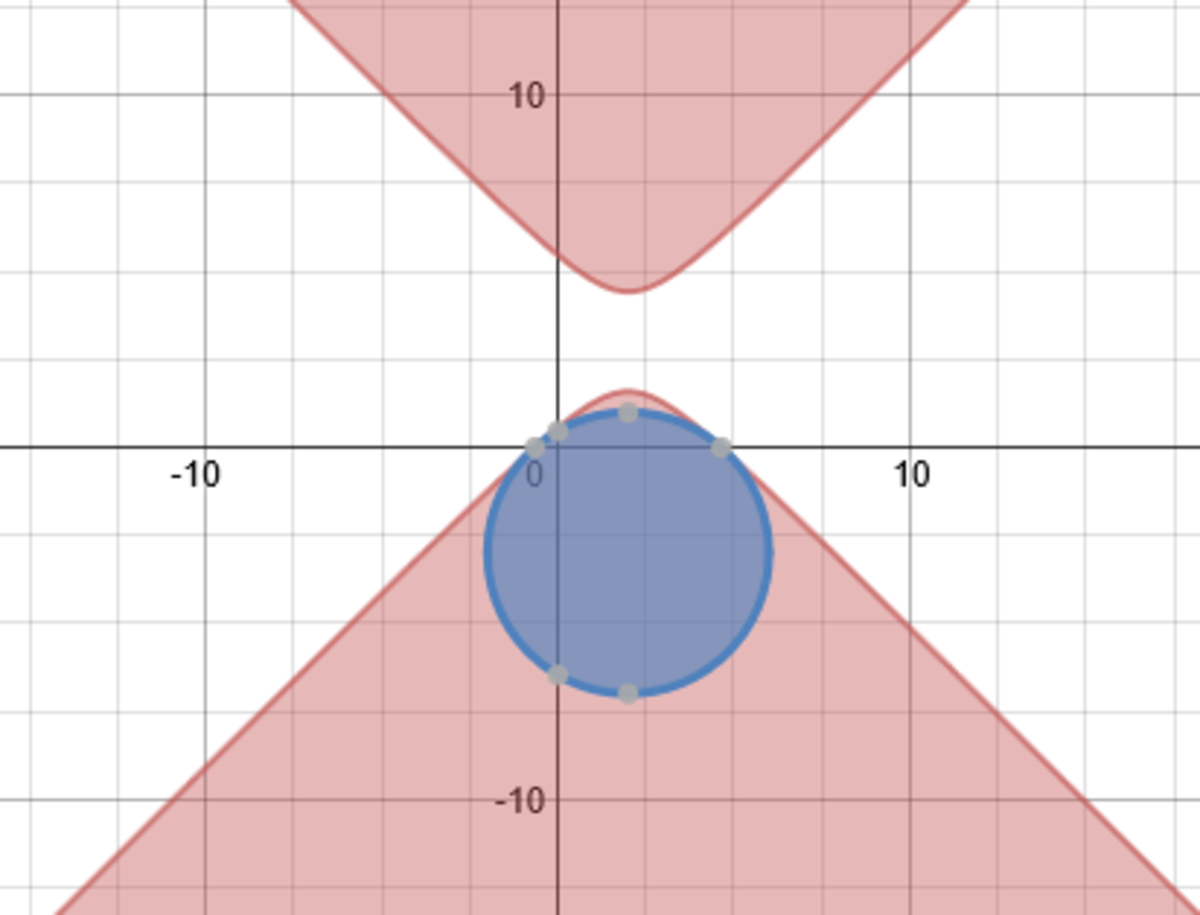
The only solution for this exercise is by graphing the inequalities and take the overlapping colors as we see in the following. Thus, the solution is all the points that belong to the circle of center ( 2 , − 3 (2,-3 ) and radius= 4 4 . By completing the square method, the equation of the circle will be ( x − 2 ) 2 + ( y + 3 ) 2 = 16 (x-2)^{2} + (y+3)^{2} = 16

1 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...