System of 3 equations

Add all the given equations to get $13x+13y+13z=26 \Rightarrow x+y+z=\dfrac{26}{13}=\boxed{2}$

$\text{Adding the three equations, we get}$

$\large \color{#3D99F6}13x+13y+13z=26$

$\text{The common factor on the left side of the equation is 13. So,}$

$\large \color{#3D99F6}13(x+y+z)=26$

$\text{Dividing both sides by 13, we get}$

$\large \boxed{\color{#3D99F6}x+y+z=13}$

Being lazy, I used the coefficients to make matrix $A = \begin{pmatrix} 1 & 2 & 4\\ 3 & 5 &7 \\ 9 & 6 & 2 \end{pmatrix}$ and the "results" of each equation in the system $B= \begin{pmatrix} 7\\ 9\\ 10 \end{pmatrix}$ and used Octave GNU to compute x = A\B. That gave the results x = 4, y = -5.5, and z = 3.5. Adding x+y+z = 2.

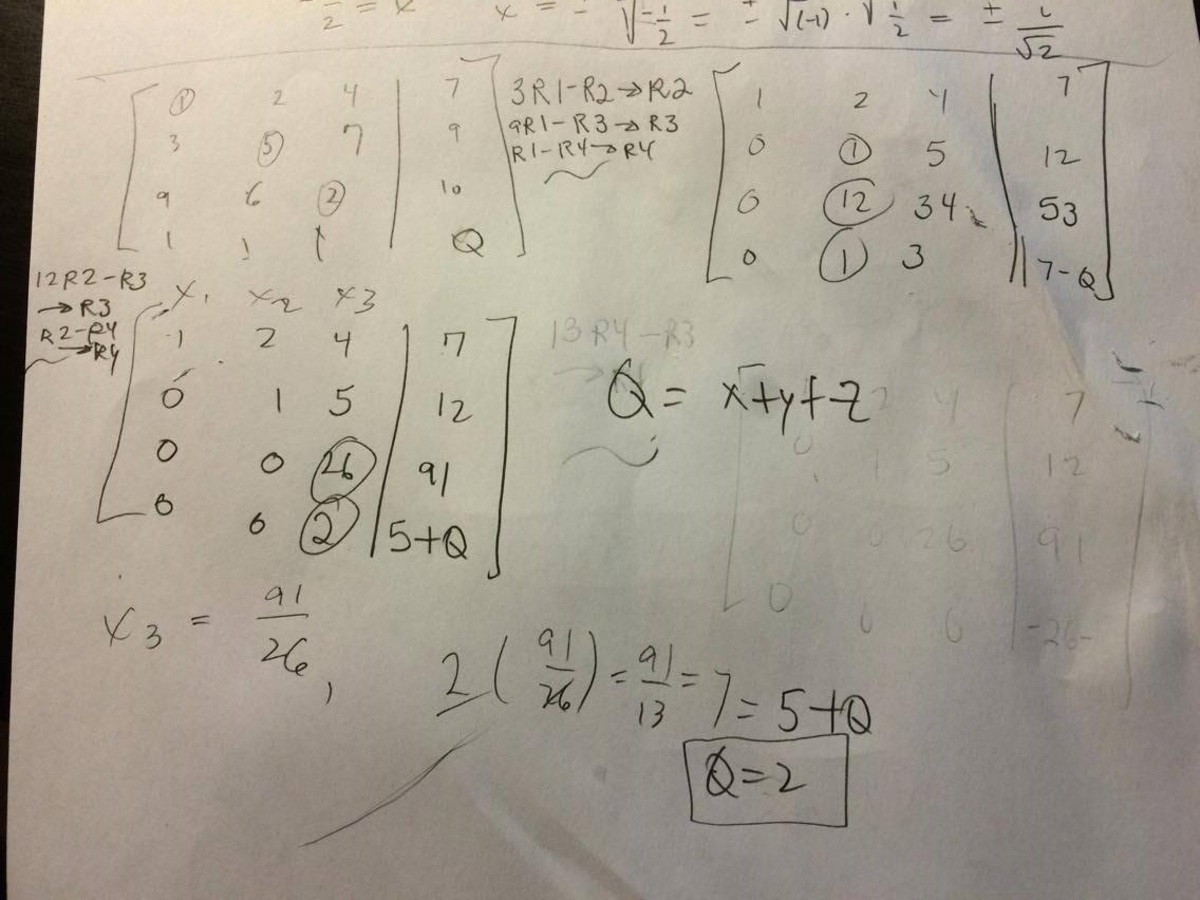
You can row reduce the augmented matrix so that everything under each pivot is 0, and then back-substitute to find x+y+z!

Row operation in order to have all 1s in a row and the result appears at the right in the augmented matrix.

x+y+z= 2 ; because 1+(-1)+2=2 I did it that way and i was totally wrong :'v

I eliminated the variables one by one until I got z=91/26 being 3.5 for Z, then back substituted to get the other two... But that's not the most efficient way.

ADD ALL EQUATION.

Same way as most on here. Add all equations Divide by 13 to isolate the variables

Adding 3 equations, 13x +13y +13z = 26; x + y + z = 26/13 = 2

Reason that this problem is of Level 2 is to guess that one needs go add all the three equations.