Solve for a and b,and add them up?

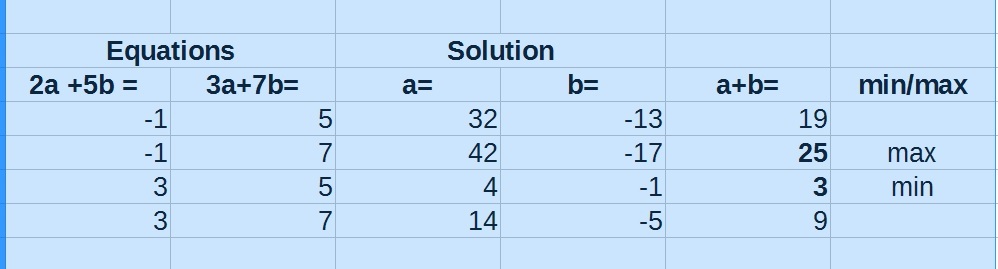
Since $3a+7b$ is not a scalar multiple of $2a+5b$ , there exist solutions to every set of simultaneous equations involving these expressions.

Note that $a+b=3(3a+7b)-4(2a+5b)$ . This means that the maximum possible value of $a+b$ is $3\times7-4\times-1=25$ and the minimum is $3\times5-4\times3=3$ .

The region in the case of this system of inequalites forms a parallelogram (similar to the one below, where I used the letters x and y instead of a and b, and changed the actual coefficients in order to see the solution better, as the original lines form a very "long and slim" parallelogram which would be hard to see on a diagram)::

We will get the solution, when we shift (parallel, so we are effectively changing the value of k in order to get the minimum and the maximum values) the line a+b=k (I used x+y=-160 on the diagram) to the vertices of the region (see the arrows).

In our case, we can determine the coordinates of the vertices of the parallelogram (region) by solving 4 pairs of simultaneous equations algebraically (with some further thought, this could be reduced to the relevant 2 pairs) and calculating the values of (a+b) in each case:

Hence, our answer should be:

$\boxed { \text { [3, 25] } }$