A calculus problem by A Former Brilliant Member
1 + 2 1 + 3 1 + 4 1 + ⋯ = ?
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Here, you started from the answer, and showed why it was correct. But how would you get the answer in the first place?
How do you know it remains true forever?
This is a very famous problem originally posed by Ramanujan
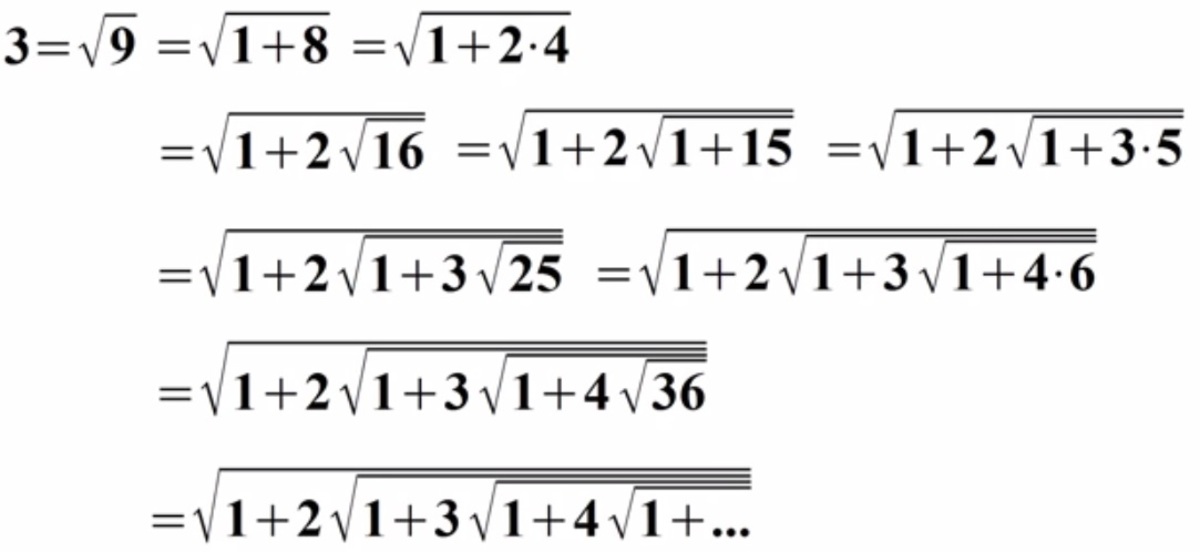
Ramanujan's formula of nested radical (eqn. 26) is as follows:
x + n + a = a x + ( n + a ) 2 + x a ( x + n ) + ( n + a ) 2 + ( x + n ) a ( x + 2 n ) + ( n + a ) 2 + ( x + 2 n ) ⋯
Putting x = 2 , n = 1 and a = 0 , we have:
2 + 1 + 0 = 1 + 2 1 + 3 1 + 4 ⋯ = 3