Solve for X
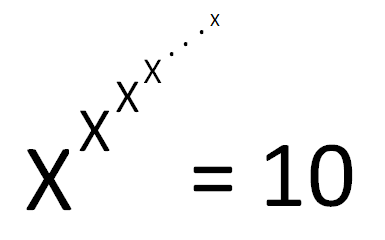 Solve for the value of X when X raised to the X until infinity to the X equals to 10.
Solve for the value of X when X raised to the X until infinity to the X equals to 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
s i m p l y s u b s t i t u t e t h e p o w e r o f x t o 1 0 s i n c e x x x ∞ = 1 0 y o u r e q u a t i o n r i g h t n o w i s x 1 0 = 1 0 , b y t h i s e q u a t i o n , y o u c a n n o w s o l v e t h e v a l u e o f x x = 1 0 1 0 x = 1 . 2 5 9
how could you find tenth root of 10
Why to substitute x to 10?
I know most of you already know this, but for the sake of the others, here's my brief solution x 1 0 = 1 0 x = 1 0 1 0 ≃ 1 . 2 5 9
can we find square root of 10 without calculator
Since this problem concerns exponents, we think of taking the logarithm on both sides. l n x x x . . . = l n 1 0 becomes x x x . . . l n x = l n 1 0 . Now, the pre-logarithmic term, x x x . . . , is equal to 10. Thus, 1 0 l n x = l n 1 0 which gives us x = e 1 0 l n 1 0 , which is actually x = 1 0 1 0 1 = 1 . 2 5 9 . . .