Solve for X in the graph and matrix below
The following picture shows a graph, , with vertices with edge set . Some edge weights are shown, and others are not.
Also below is the resulting matrix from the Floyd-Warshall algorithm . In this matrix, shows the distance between vertex and vertex in the graph. Solve for .
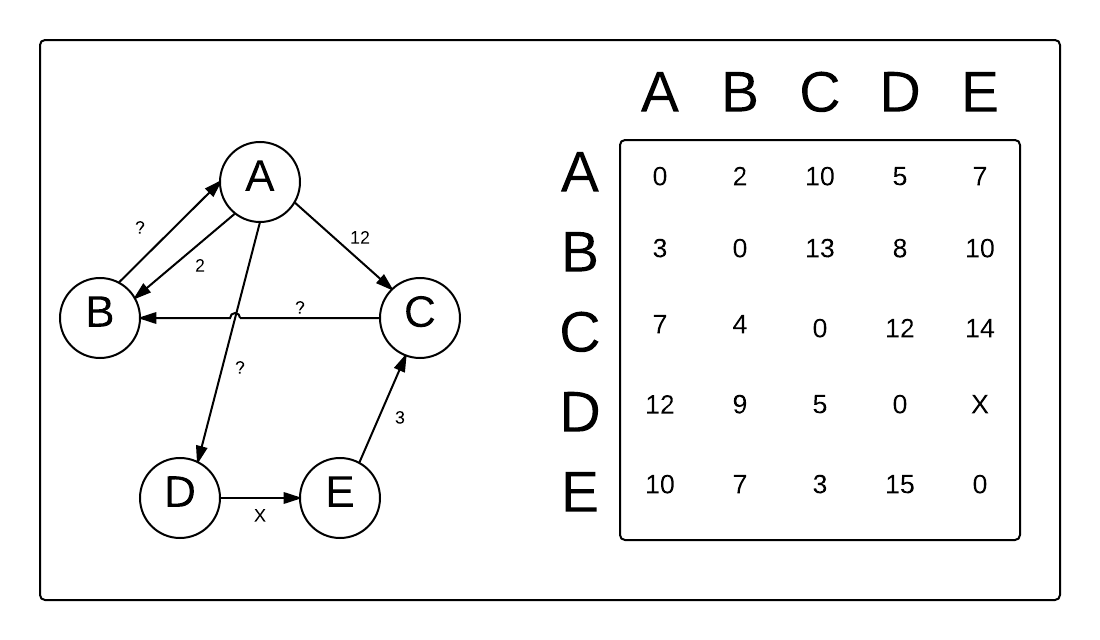 Graph and distance matrix
Graph and distance matrix
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Using the provided matrix we can see the distance from D to C is 5 and the only path is D=>E=>C, and the distance from E to C is 3. If the total distance from D to C is 5 and the distance from E to C is 3, then X has to be 2.