This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Moderator note:
I wonder if there is a better reason why the answer is 4 1 . Maybe looking at cos 1 3 θ , or the 13th roots of unity, would help.
@Alan Enrique Ontiveros Salazar good question!!!!
Let w = e 2 π i / 1 3 , then let's use the product to sum formulas:
2 1 [ cos ( 1 3 8 π ) + cos ( 1 3 4 π ) + cos ( 1 3 1 0 π ) + cos ( 1 3 6 π ) + cos ( 1 3 1 4 π ) + cos ( 1 3 2 π ) ] .
But cos ( 1 3 1 4 π ) = cos ( 1 3 1 2 π ) , so:
2 1 [ cos ( 1 3 2 π ) + cos ( 1 3 4 π ) + cos ( 1 3 6 π ) + cos ( 1 3 8 π ) + cos ( 1 3 1 0 π ) + cos ( 1 3 1 2 π ) ]
With the fact that 2 1 ( w k + w 1 3 − k ) = cos ( 1 3 2 π k ) and w + w 2 + ⋯ + w 1 1 + w 1 2 = − 1 , which follows inmediatly from factoring w 1 3 = 1 we get:
2 1 ( 2 w + w 1 2 + w 2 + w 1 1 + w 3 + w 1 0 + w 4 + w 9 + w 5 + w 8 + w 6 + w 7 ) 2 1 ( 2 − 1 )
So, cos ( 1 3 2 π ) cos ( 1 3 6 π ) + cos ( 1 3 2 π ) cos ( 1 3 8 π ) + cos ( 1 3 6 π ) cos ( 1 3 8 π ) = − 4 1
On comparing we get α = 1 , β = 4 , thus the final answer is 1 + 4 = 5 .
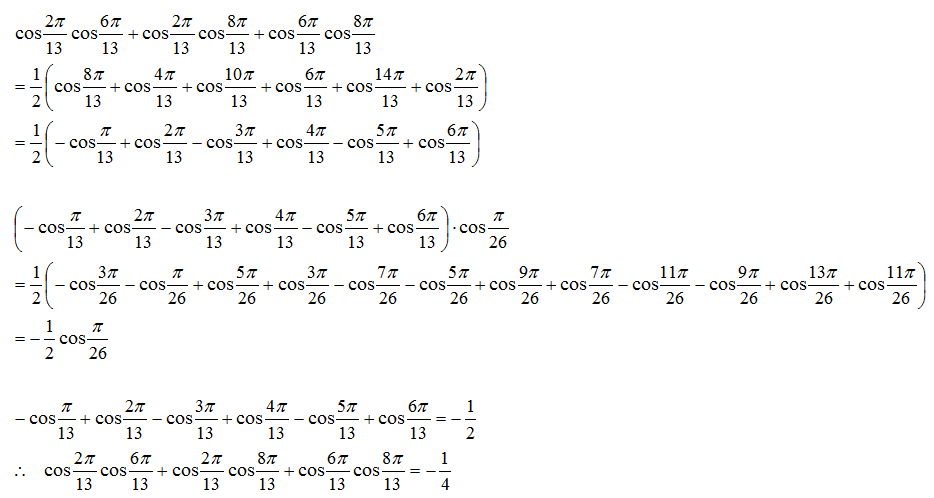
cos ( 1 3 2 π ) cos ( 1 3 6 π ) + cos ( 1 3 2 π ) cos ( 1 3 8 π ) + cos ( 1 3 6 π ) cos ( 1 3 8 π ) = 2 1 [ 2 cos ( 1 3 2 π ) cos ( 1 3 6 π ) + 2 cos ( 1 3 2 π ) cos ( 1 3 8 π ) + 2 cos ( 1 3 6 π ) cos ( 1 3 8 π ) ] = 2 1 [ cos ( 1 3 2 π ) cos ( 1 3 6 π ) − sin ( 1 3 2 π ) sin ( 1 3 6 π ) + cos ( 1 3 2 π ) cos ( 1 3 6 π ) + sin ( 1 3 2 π ) sin ( 1 3 6 π ) + cos ( 1 3 2 π ) cos ( 1 3 8 π ) − sin ( 1 3 2 π ) sin ( 1 3 8 π ) + cos ( 1 3 2 π ) cos ( 1 3 8 π ) + sin ( 1 3 2 π ) sin ( 1 3 8 π ) + cos ( 1 3 6 π ) cos ( 1 3 8 π ) − sin ( 1 3 6 π ) sin ( 1 3 8 π ) + cos ( 1 3 6 π ) cos ( 1 3 8 π ) + sin ( 1 3 6 π ) sin ( 1 3 8 π ) ] = 2 1 [ cos 1 3 8 π + cos 1 3 4 π + cos 1 3 1 0 π + cos 1 3 6 π + cos 1 3 1 4 π + cos 1 3 2 π ] = 2 1 [ cos 1 3 2 π + cos 1 3 4 π + cos 1 3 6 π + cos 1 3 8 π + cos 1 3 1 0 π + cos 1 3 1 2 π ] = 2 1 [ − 2 1 ] [ See Note ] = − 4 1 ⇒ a + b = 1 + 4 = 5
Note: z 1 3 = e 1 3 2 π = 1 are the 13 t h roots of unity. By Argand's diagram, we can see that: cos 1 3 2 π + cos 1 3 4 π + cos 1 3 6 π + cos 1 3 8 π + cos 1 3 1 0 π + cos 1 3 1 2 π = − 2 1