solve it iq of 115
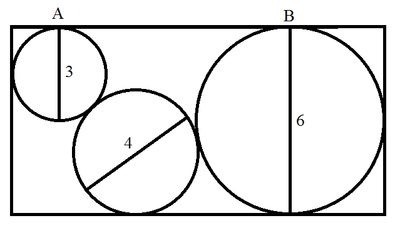
As shown in the figure, circle of diameter 4 touches the other two circles and the bottom of the rectangle. Circle of diameter 3 touches the top at A and left side of the rectangle. Circle of diameter 6 touches the top at B and two other sides of the rectangle. Find the length of A B .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Chew-Seong Cheong sir, please edit the question as moderator so that it no longer says that the radii of the circles are 3,4, and 6. It should actually be that the diameter of the circles are 3,4, and 6. Thank you sir!
The length of A B is the sum of two distances, namely, the horizontal distance between the centres of the left and the middle circle, which is equal to ( 3 . 5 ) 2 − ( 2 . 5 ) 2 = 6 and the horizontal distance between the middle and the right circles, which is equal to ( 2 + 3 ) 2 − 1 2 = 2 6 . Thus the required distance is 3 6
The original problem states that the radii of the circles are 3,4,and 6. The solution is based on the diameter of those circles being 3,4,6.
The process of elimination is the most useful in this question.
We know that AB must be around 7 units long (4+3), therefore the first answer, 6 , is not right.
Likewise, the second option, 3.5 is not right either, because it is much less than AB.
The third option, 3 5 3 6 , is not right, because it is almost the same length as the radius of the 6 diameter circle.
Therefore, the last option, 3 6 must be right, as it is just greater than 7 units, being 7 . 3 4 , as expected.
No Pythagoras or any fancy stuff required!
Let O be the center of circle of radius 4. We note that
A B = A ′ O + B ′ O = ( 2 7 ) 2 − ( 2 5 ) 2 + 5 2 − 1 2 = 6 + 2 6 = 3 6 By Pythagorean theorem
Reference: Pythagorean theorem