Solve it like a Mathematician.

Cast problem into co-ordinate plane. The points are in horizontal line with $z_1(10,6) \text{ and } z_2(4,6)$ . Now, the given condition implies that the arrow joining $z_1 \text{ to } z$ (arrow at latter) on rotation by $\pi/4$ clockwise will point in the same direction as the arrow joining $z_2 \text{ to }z$ . Since the points are $6$ units from each other, obviously $z=4+12i$ satisfies given condition(the points form an isosceles right triangle).

Hence: $|z-7-9i|=|4-7+12i-9i|=|-3+3i|=3 \sqrt{2}$

Classic JEE style strikes again.

Edit: If one is really well versed in complex geometry, one can see that the locus described by $z$ is a part of a circle. The point $7+9i$ is the center of circle, and hence, the answer is simply distance of one of the given points from center(radius) as both given points and $z$ lie on circle.

Let $z = a + bi$ then, we have:

$\begin{aligned} \dfrac {z-z_1}{z-z_2} & = \dfrac {(a-10)+(b-6)i}{(a-4)+(b-6)i} \\ & = \dfrac {[(a-10)+(b-6)i ][(a-4)-(b-6)i]}{(a-4)^2+(b-6)^2} \\ & = \dfrac {(a-10)(a-4)+(b-6)^2 +(b-6)(a-4-a+10)i}{(a-4)^2+(b-6)^2} \\ & = \dfrac {a^2+b^2-14a-12b+76 + (6b-36)i}{(a-4)^2+(b-6)^2} \end{aligned}$

Since $\space \arg {\left(\dfrac {z-z_1}{z-z_2}\right)} = \dfrac {\pi}{4}\quad \Rightarrow \dfrac {6b-36} {a^2+b^2-14a-12b+76} = 1$

$\Rightarrow 6b-36 = a^2+b^2-14a-12b+76 \\ \Rightarrow a^2+b^2-14a-18b = -112$

Now,

$\begin{aligned} | z-7-9i| & = \sqrt{(a-7)^2+(b-9)^2} \\ & = \sqrt{a^2+b^2-14a-18b+49+81} \\ & = \sqrt{-112+49+81} \\ & = \sqrt{18} = \boxed{4.243} \end{aligned}$

Check yhe solution in image

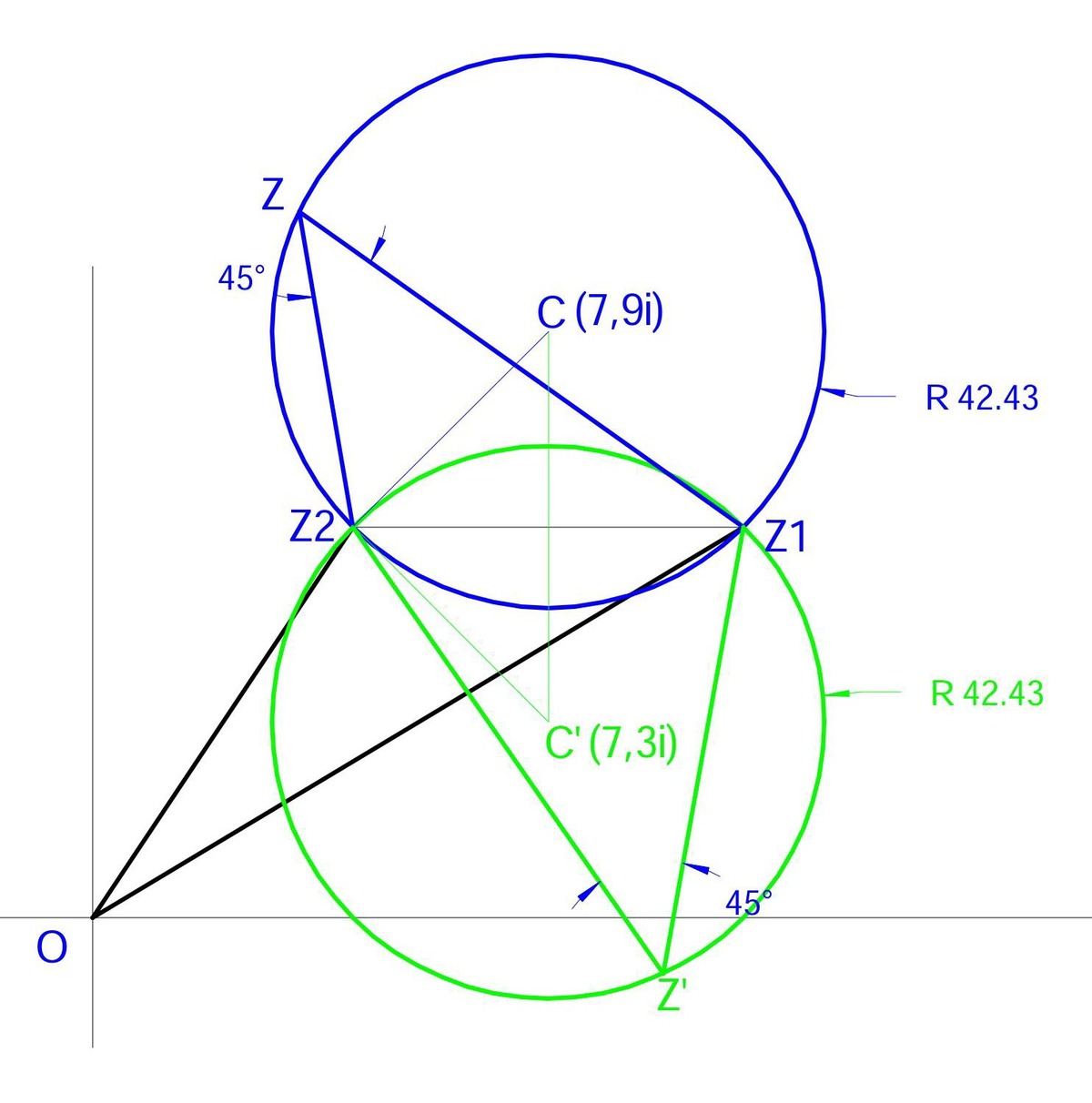Being the argument of division of the two complex pi/4, means that z must be in circumference which center is or 7➕9i or 7➖3i, passing over z1 and z2, since from z you see that point z1 and z2 form a 45 degree angle. Obviously the radius is Sqrt( 3^2+ 3^2).

Cunningly the poster has chosen one of the possible centers only points in which the modulus of the two complex remains constant for any z located in the mentioned circunferences.

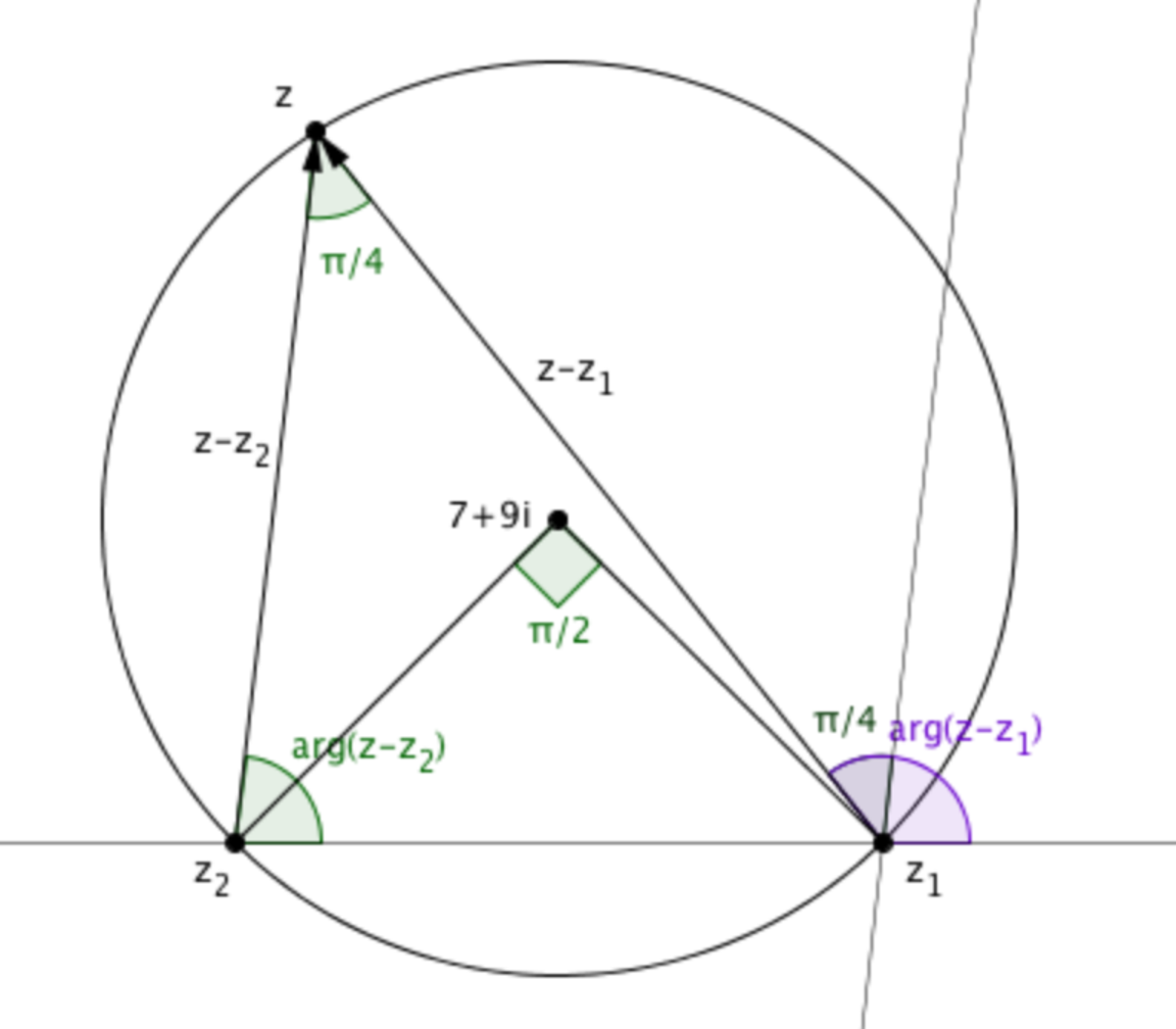Same as other solution, with a little more detailed image to see the angles.

nice question!

I will describe the locus of the condition given, in a general way that works for almost (if not all) any Möbius transformation. This trick is extremely common and useful in complex geometry, although in this example it seems over-complicated and unnecessary, but it is worth to be mastered.

First let $f(x)=\frac{z-z_1}{z-z_2}$ . By hand or by formula, it is easy to see $f^{-1}(x)=\frac{(10+6i)-(4+6i)z}{1-z}$ and look at the image of $\{z:arg(z)=\frac{\pi}{4}\}$ under $f^{-1}$ .

Since Möbius transformations preserves generalised circles, which are determined uniquely by $3$ points, note that $0, 1+i, \infty$ get mapped to $10+6i, 4+12i, 4+6i$ by $f^{-1}$ , so the image we are looking for is the circular arc with endpoints $10+6i, 4+6i$ passing though $4+12i$ . The perpendicular bisectors of the first/third points and second/third points are $Re(z)=7, Im(z)=9$ respectively, hence the locus is this circular arc described centered at $7+9i$ with radius $\sqrt{18}$ , which value is $4.243$ answering the question.

One may argue the inverse was not necessary to be found, and could just solve $f(z)=0,1+i,\infty$ easily (especially for $0$ and $\infty$ ), but since I remember the formula for the inverse, that is what I did.