Solve $x^y = y^x$

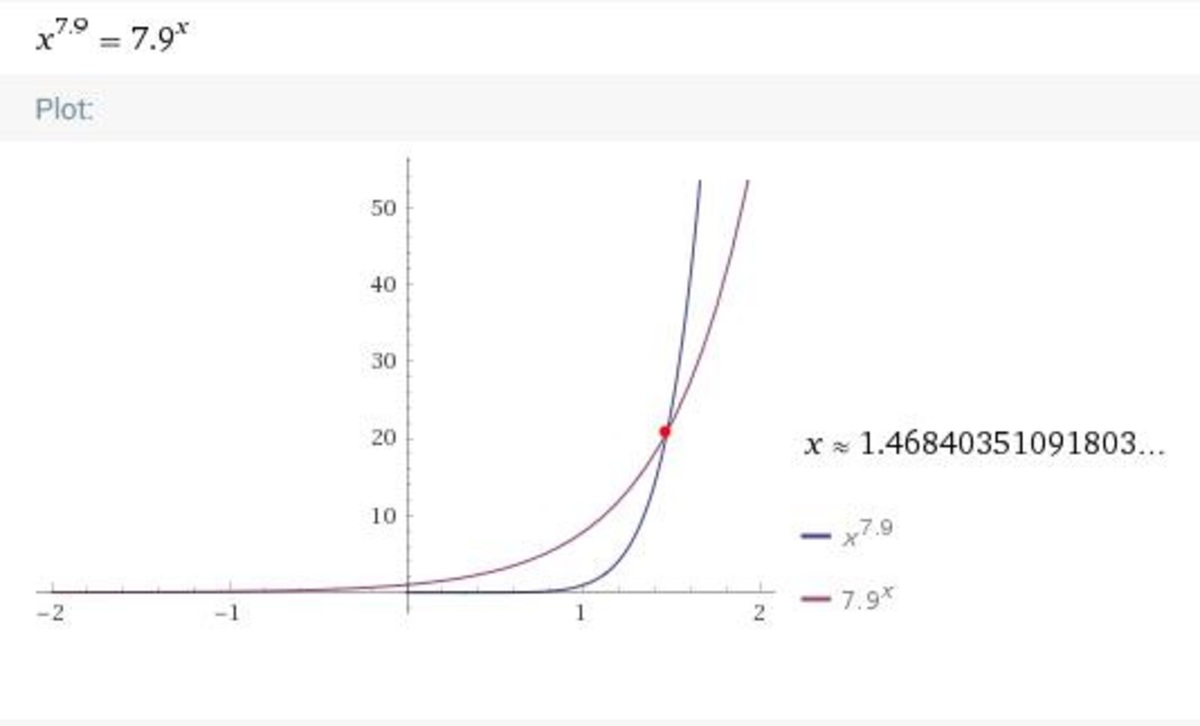
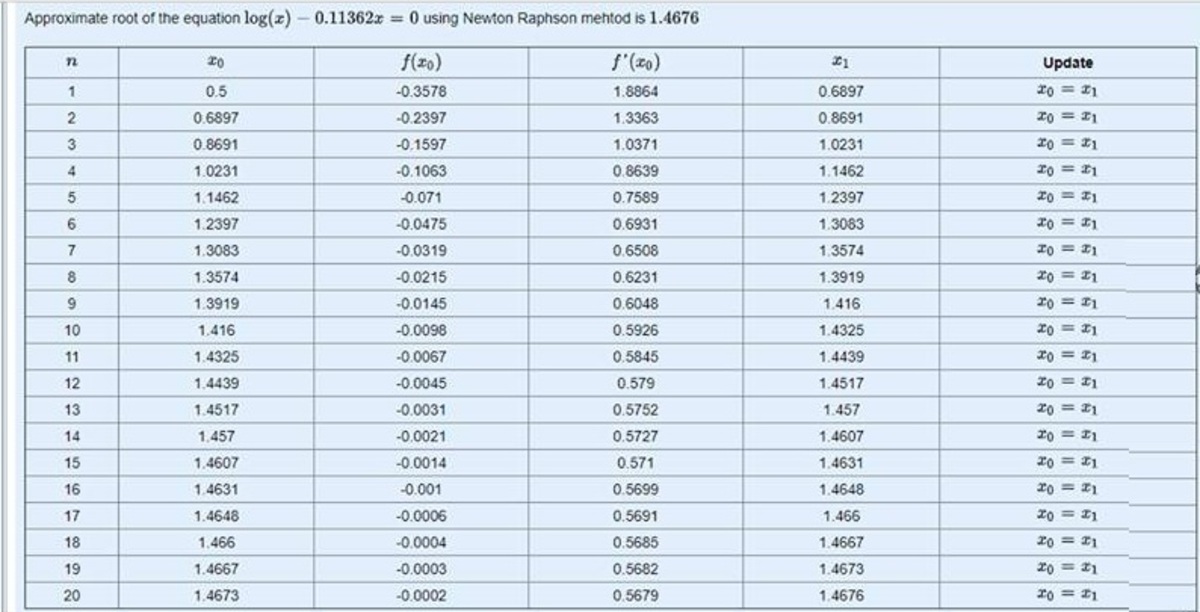
Taking natural logarithm on both sides of $x^{7.9} = 7.9^x$ , we have $7.9\ln x = x \ln 7.9$ . Let $f(x) = 7.9\ln x - x \ln 7.9$ . Then $f'(x) = \dfrac {7.9}x - \ln 7.9$ . Using Newton-Raphson method , we have $x_{n+1} = x_n - \dfrac {f(x_n)}{f'(x_n)}$ , we get $x \approx \boxed{1.468403511}$ .

The following is the calculations with an Excel spreadsheet. Column A: $x_n$ , column B: $f(x_n)$ , column C: $f'(x_n)$ , and column D: $x_{n+1}$ .

Solving graphically

Solving by the Newton Raphson's method

The solution using Newton Raphson's method yields a mod(ε) of 0.055 whereas the solution arrived at using the Graphical method yields a lower mod(ε) of 0.00024 , so the solution to the above equation is x = 1.4684