Count The Right Triangles!
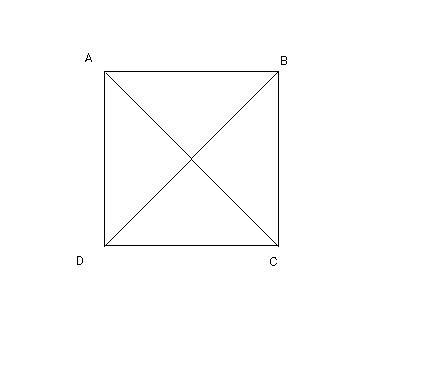 How many right angled triangles are there in the diagram above?
How many right angled triangles are there in the diagram above?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
11 solutions
there r 8 right angles because 4 are intersacting and 4 are corners
How do u noe that the diagonals intersect each other perpendicular to each other, it is not mentioned nor is it mentioned that the quadrilateral is a square?
Log in to reply
In a square, diagnols bisect and are perpendicular to each other
it isnt given whether it is a square or an irregular quadrilateral
There are 2 perpendicular diagnolas=>4 right angled triangles are there.If we see two diagonals individually then we get another 4 right angled triangles.
pleas explain in urdu language please. i don not understand
Log in to reply
Use Google Translator. Copy the English text and choosse Urdu.
How do u noe that the diagonals intersect each other perpendicular to each other, it is not mentioned nor is it mentioned that the quadrilateral is a square?
If nd = 2, is the number of diagonals, for every diagonal there are 2 right angled triangles, and every triangle is subdivided in 2 right angled triangles by the other diagonal, so, the number of triangles is:
Nt0 = 2 x2 + 2 x 2 = 2 x 2^2 = 2^3 = 8
If we divide the square in 4 equal squares, and draw the diagonals for the major square and for every subsquare, the number of right angled triangles is:
Nt1 = 8 + 4 x 8 = 5 x 8 = 40;
The number of division in elementary subsquares (not further divided) at the step n, is 4^n, so there are a number of right angled triangles by the subdiagonals:
Nt(n) = 8 + 4 x 8 + 4 x 4 x 8 +…+ (4^n) x 8 =
Nt(n) = 8{Σ[(k = 0; n)(4^k)]} =
Nt(n) = 8(4^(n + 1) – 1)/(4 – 1) =
Nt(n) = (8/3)[4^(n + 1) – 1];
ok try again
whats his question?
Consider the secant lines in the square. They make 4 right triangles, their (common) right angle being the intersection of the 2 perpendicular lines (in the center of the square). Then, we can see that by coupling two of these triangles, which share a common side, we get another right triangle. Since the square has 4 sides, we can conclude that there are 4 such triangles. So in the end you have 4 + 4 = 8.
the answer is 8, there are eight right triangles
Label center O The triangles are: AOB,BOC,DOC,AOD,ABC,BDC,ADC and ADB
Draw the midpoint AB to DC, passing by the intersection of the diagonals, and draw the midpoint AD to BC, passing by the same intersection before. Now you can see 8 right angled triangles.
I assumed the diagram was a square, but the problem does not explicitly say this. If the quadrilateral were a rectangle instead, the answer would only be 4, as the diagonals cannot be assumed to form 45-degree angles with the corners.
4 right angles in the centre, 4 right angles around the outer edge of the square. 8 triangles can be made using these 8 right angles.
Just in case,if anyone is a fan of combinatorics..he might follow this approach.. Total number of right triangles = 5 C 3 - 2 ,we Subtracted two for the case when the three points are on the diagonal

There are four obvious triangles having vertices as ABC, ADC, ADB, BDC.
In addition to these, four triangle are more due to the right angles at the centre viz. ODC, OCB, OAB, and OAD where O is the centre.