Solve this if you can!!
Geometry
Level
2
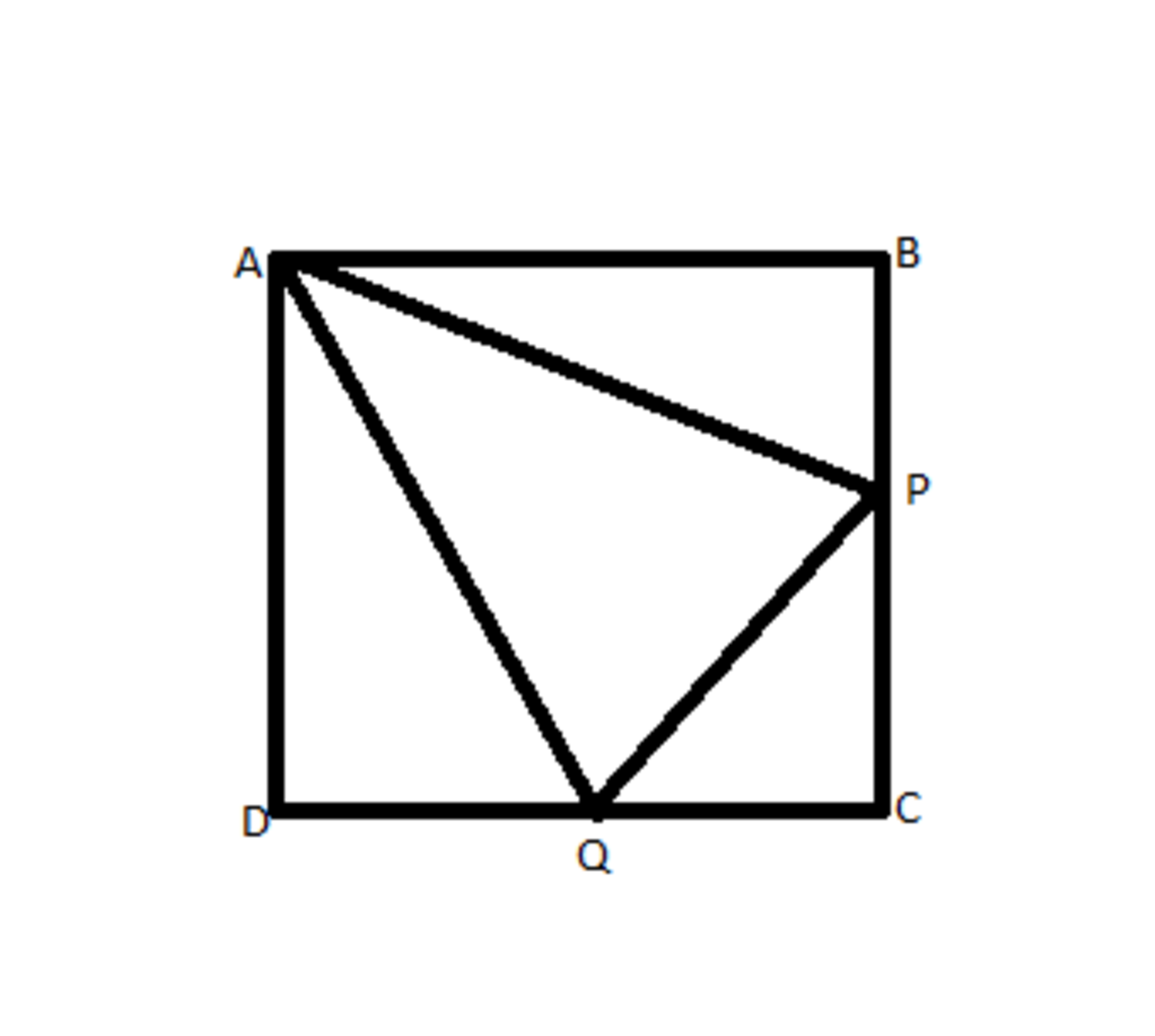ABCD is a square. P and Q are points on CD and BC respectively such that
. AB = 1 unit. Find the perimeter of triangle PQC.
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Let length of DP be a units. Then length of PC = (1 - a) units. Let length of BQ be b units. Then length of QC = (1-b) units. Now in triangle ADP, tan DAP = a and in triangle ABQ, tan BAQ = b. angle DAB = 90 degree. PAQ = 45 degree. Then, angle DAP + angle BAQ = 45 degree. So, (1+tan DAP)(1+tan BAQ)= 2. that implies (1 + a)(1 + b) = 2 that implies a + b + ab = 1. Then ab can be written as (1-a-b).
angle C = 90 degree. By applying Pythagoras theorem, PQ^2 = (1-a)^2 + (1-b)^2 this gives PQ^2 = (1 + a^2 - 2a + 1 + b^2 - 2b)^ 2 that implies PQ^2 = [2(1 - a - b) + a^2 + b^2]^2. But we know that ab = (1 - a - b). So, PQ^2 = [a^2 + b^2 + 2ab]^2. This gives PQ = (a + b). Thus, perimeter of PQC = (1-a) + (1-b) + (a + b) = 1 +1 = 2 units.