Solve this mentally

We all know the $GM^{2}$ = $AM \times HM$ part. So I'll just get to the derivation of it.

We know that

GM= $\sqrt{ab}$

AM= $\frac{a+b}{2}$

HM= $\frac{2ab}{a+b}$

$\frac{2ab}{a+b}$ = $\frac{\sqrt{ab} \times \sqrt{ab}}{\frac{a+b}{2}}$

$HM= GM^{2} \times \frac{1}{AM}$

$GM^2=AM*HM$
This is not a full solution just a hint until I post the proof. Edit AM>GM>HM To find the relation between AM,GM,HM let us consider two numbers "a"and "b"

AM = 0.5(a+b)

GM = (ab)^0.5

HM = 2ab/a+b

Now by observation AM*HM = GM^2 so now that we have proven this it just substitute and solve. $GM^2=AM*HM$ $(6^2)/10)=3.5$

AM * HM = GM^2

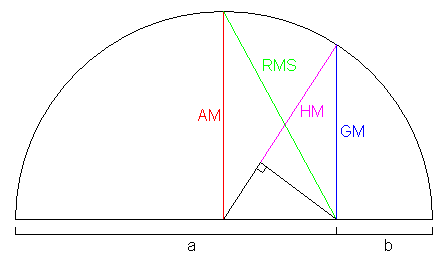
Trigonometrically, you can conclude that: $\frac{GM}{AM}=\frac{HM}{GM}$ This means that: $HM=\frac{{GM} \times {GM}}{AM}$ or: $HM=\frac{{6} \times {6}}{10} = 3.6$

We have that AM = a+b/2 = 10 thus a+b = 20, GM = (ab)^1/2 = 6 thus ab = 36, Substitute b = 20-a, then we have a(20-a) = 36, Solve with quadratic equation, we have a= 18, b = 2 or a = 2, b = 18, HM = 2/(1/a+1/b) = 2/(1/18+1/2) = 2/10/18=3.6

From the given, we can find solve for a+b and ab

a+b = 20 ab = 36

^pretty much common sense

1/a + 1/b = (b+a) / (ab)

AM of the reciprocals = ((b+a) / (ab))/2 = (b + a) / (2ab) = (2(36))/(2ab)

get the reciprocal of the AM to get the HM --> 2ab / b + a = 3.6

:)))))