Solving differential equations using circuits
The following circuit solves a 2nd order homogenous ODE ,
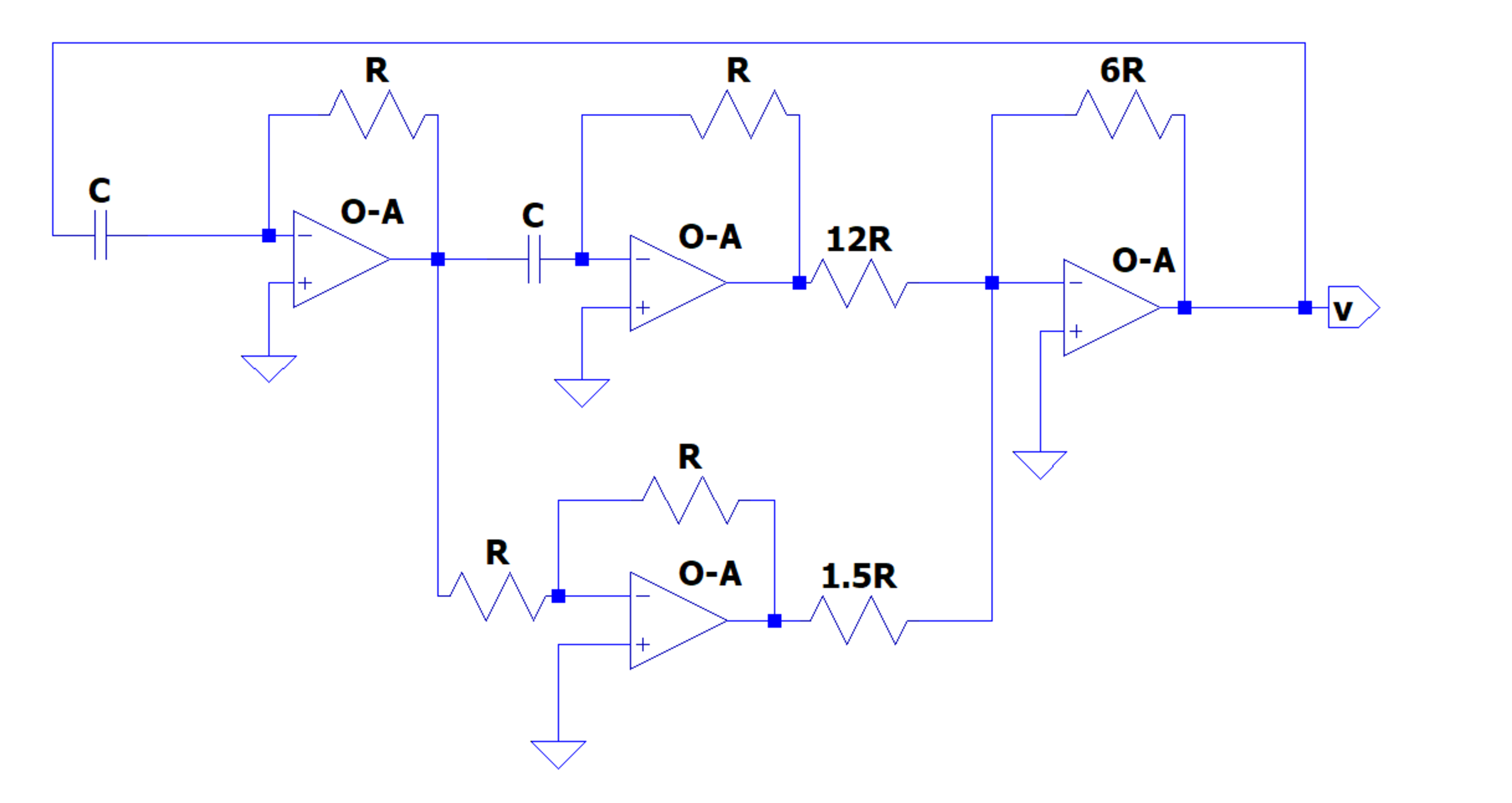
R is the resistance value and C is the capacitance value. Find the sum of coefficients of the differential equation in standard form if
Assume Op-Amps are ideal, with infinite |Vcc|
The answer is 11.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
To make it possible to follow the solution, I have labeled intermediate quantities in the diagram. Recall the two "golden rules" of op amps in the inverting feedback configuration:
1) The voltages at the inputs are equal
2) The currents into the inputs are zero
Proceed to solve for the quantities:
I 1 = C V ˙ V 1 = 0 − R I 1 = − R C V ˙ I 2 = C V ˙ 1 = − R C 2 V ¨ V 2 = 0 − R I 2 = R 2 C 2 V ¨ I 4 = 1 2 R V 2 = 1 2 R C 2 V ¨ I 3 = R V 1 = − C V ˙ V 3 = 0 − R I 3 = R C V ˙ I 5 = 1 . 5 R V 3 = 1 . 5 C V ˙ I 6 = I 4 + I 5 = 1 2 R C 2 V ¨ + 1 . 5 C V ˙
Having determined the intermediate quantities, we can now write a final expression for V .
V = 0 − 6 R I 6 = − 6 R ( 1 2 R C 2 V ¨ + 1 . 5 C V ˙ ) V = − 2 R 2 C 2 V ¨ − 4 R C V ˙
Simplifying a bit more, and substituting in R C = 1 , results in:
V ¨ + 8 V ˙ + 2 V = 0