Solving the heat equation

Calculus Level 5

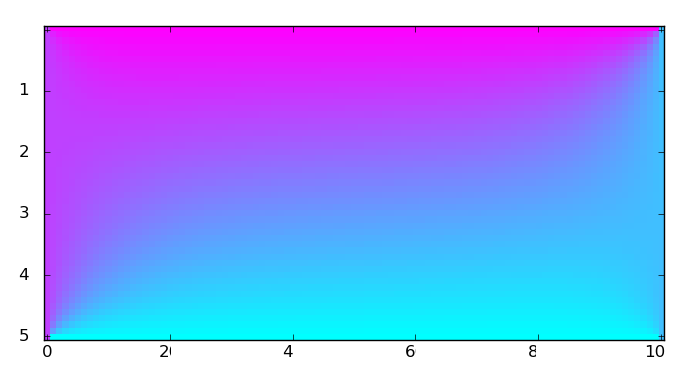
A two-dimensional non-transient rectangular system follows the heat equation $\nabla^2 T = 0$ where $T(y,x)$ is the temperature at $(y,x)$ .

The system is 5 units wide (vertical) and 10 units (horizontal).
The temperatures of north, east, west and south walls are maintained at 100, 40, 80 and 20 respectively.

What is the temperature of a point located 4 units to the right of the west wall and 2 units to the bottom of the north wall?

Note : This problem might require a numerical approach.

Inspired by Himadri Chattopadhyay .

The answer is 68.698.

1 solution

Agnishom Chattopadhyay
Jul 18, 2016

[Partial Solution]

I do not remember the entire process of solving the problem but the crux of this solution is to divide the area into a discrete grid. Provided the grid is small enough, i.e, as the cell size approaches 0, the heat equation is equivalent to the fact that every point is equal to the mean of the four points around it.

We represent this grid as a two-dimensional array with the boundaries initialized. The non-boundary cells are initialized with some arbitrary temperature. With each iteration, each cell is updated as the mean of the neighbouring cells. These are called Jacobi iterations. Ultimately, the values in the cells converge to the steady solution.

import numpy
import matplotlib.pyplot

class System:
    def __init__(self,length,height,gridSize):
        self.length = length
        self.height = height
        self.gridSize = gridSize
        self.grid = numpy.empty((self.height/self.gridSize + 1, self.length/self.gridSize + 1,))
        self.__str__ = self.grid.__str__
    def plot(self,name):
        matplotlib.pyplot.clf()
        matplotlib.pyplot.imshow(self.grid, cmap='cool', interpolation='nearest')
        matplotlib.pyplot.savefig(name)
    def plotConvergence(self,name):
        matplotlib.pyplot.clf()
        matplotlib.pyplot.plot(sys.errorHistory[1:])
        matplotlib.pyplot.savefig(name)
    def boundaryInit(self, north, east, west, south):
        self.grid[:] = min([north,east,west,south])
        self.grid[0,] = north
        self.grid[self.height/self.gridSize] = south
        self.grid[:,0] = west
        self.grid[:,self.length/self.gridSize] = east
    def iterate(self,fittingFactor=1):
        self.it += 1
        for i in xrange(1,int(self.height/self.gridSize)):
            for j in xrange(1, int(self.length/self.gridSize)):
                new = (self.grid[i+1,j] + self.grid[i,j+1] + self.grid[i-1,j] + self.grid[i,j-1])/4.0
                self.grid[i,j] = self.grid[i,j] + (new - self.grid[i,j])*fittingFactor
    def solve(self, prec,fittingFactor=1):
        self.it = 0
        oldSum = numpy.sum(abs(self.grid[1:self.height/self.gridSize, 1:self.length/self.gridSize]))
        newSum = 123
        self.errorHistory = []
        while True:
            oldSum = newSum
            self.iterate(fittingFactor)
            newSum = numpy.sum(abs(self.grid[1:self.height/self.gridSize, 1:self.length/self.gridSize]))
            error = abs(newSum - oldSum)/((self.height/self.gridSize - 1)*(self.length/self.gridSize - 1))
            self.errorHistory.append(error)
            if error <= prec:
                break

sys = System(10,5,0.1)
sys.boundaryInit(100,40,80,20)
sys.solve(0.001,1.2)

sys.plot("solution12.png")
sys.plotConvergence("error.png")
print sys.grid[20,40]

Since we want the temperature at an integral coordinate and the lengths of all walls are integers, it suffices to run the Jacobi iteration on the lattice grid, consisting of $4\times 9=36$ lattice points only. In other words, smaller grid sizes are unnecessary. This hugely speeds up the procedure.

Abhishek Sinha - 4 years, 10 months ago

Solving the heat equation

Inspired by Himadri Chattopadhyay .

The answer is 68.698.

1 solution

0 pending reports