Solving the series
Recall that
e
x
=
1
+
1
!
x
+
2
!
x
2
+
3
!
x
3
+
⋯
.
Then what is the value of
1
!
2
+
3
!
4
+
5
!
6
+
⋯
3
!
2
+
5
!
4
+
7
!
6
+
⋯
?
Notation:
!
is the
factorial
notation. For example,
8
!
=
1
×
2
×
3
×
⋯
×
8
.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Moderator note:
The solution uses the "trick" that n ! n simplifies to ( n − 1 ) ! 1 .
In a similar vein, can you evaluate ∑ i = 1 n i × i ! as a telescoping sum?
Nice solution! I like how you split each fraction as sum/difference of two fractions. What motivated you to split the fractions the way you did?
S n = ∑ i = 1 N i × i ! = 1 . 1 ! + 2 . 2 ! + 3 . 3 ! + 4 . 4 ! + 5 . 5 ! + 6 . 6 ! + ⋯ N . N !
S n = ∑ i = 1 N = 1 + 4 + 1 8 + 9 6 + 6 0 0 + 4 3 7 0 + ⋯ N . N !
S n = ( 2 − 1 ) + ( 6 − 2 ) + ( 2 4 − 6 ) + ( 1 2 0 − 2 4 ) + ( 7 2 0 − 1 2 0 ) + ( 5 0 4 0 − 7 2 0 ) + ⋯ + ( n + 1 ) ! − ( n − 1 ) !
S n = ( 2 ! − 1 ! ) + ( 3 ! − 2 ! ) + ( 4 ! − 3 ! ) + ( 5 ! − 4 ! ) + ( 6 ! − 5 ! ) + ( 7 ! − 6 ! ) + ⋯ + ( ( n + 1 ) ! − ( n − 1 ) ! )
S n = − 1 ! + ( 2 ! − 2 ! ) + ( 3 ! − 3 ! ) + ( 4 ! − 4 ! ) + ( 5 ! − 5 ! ) + ⋯ + ( n − 1 ) ! − ( n − 1 ) ! + ( n + 1 ) !
Since all the terms get cancelled except − 1 and ( n + 1 ) ! which shows that ∑ i = 1 N i × i Is a telescoping series which is equal to
S n = ( n + 1 ) ! − 1
Log in to reply
Last term should be ((n+1)! - (n)!) so that it cancel out with n! from the previous term. It shouldn't be ((n+1)! - (n-1)!).
Also typo in the first line in the solution for original question, (i+1)! = (i+1)(i!)
@Pi Han Goh Thank you , Sir :)
We can see that
( i + 1 ) ! = i ! ( i + 1 ) ! = i × i ! + i !
Then
i × i ! = ( i + 1 ) ! − i !
And we have that
∑ i = 1 n i × i ! = ∑ i = 1 n ( ( i + 1 ) ! − i ! )
This is a telescopic sum, that is, only the values − 1 ! and ( n + 1 ) ! remain, the rest cancel out. So in the end
∑ i = 1 n i × i ! = ( n + 1 ) ! − 1
Log in to reply
Yup, that's just telescoping sum in disguise! Well done~~
There's a typing mistake in the first line.
Did the same as Naren's solution.
Thank you for the compliment :) Well, there is no such any motivation however for the numerator terms and denominator i just tried to expend so that i could get exact match with e x series. Moreover, the term in numerator are the pattern of n + 1 ) ! n and better spliting the factorial part i splited without factoriart part . :)
WolframAlpha
(sum(2n/(2n+1)!), n=1 to infinity)/(sum(2n/(2n-1)!), n=1 to infinity)
= 0.135335
Impressive skill.
Let
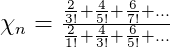
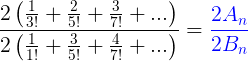
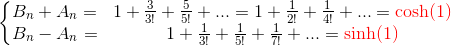
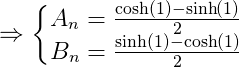
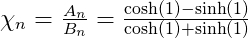 And after simplification, we get
And after simplification, we get
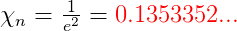
Ah nice! It's nice that we can express the numerator and denominator as an expression of hyperbolic trigonometric functions!
Aren't you missing the term 3 ! 2 in your second line?
Practice L a T E X soon.
Evaluating the numerator as :- 3 ! 2 + 5 ! 4 + 7 ! 6 + ⋯
3 ! 3 − 1 + 5 ! 5 − 1 + 7 ! 7 − 1 + ⋯
3 ! 3 − 3 ! 1 + 5 ! 5 − 5 ! 1 + 7 ! 7 − 7 ! 1 + ⋯
2 ! 1 − 3 ! 1 + 4 ! 1 − 5 ! 1 + 6 ! 1 − 7 ! 1 + ⋯
1 − 1 ! 1 + 2 ! 1 − 3 ! 1 + 4 ! 1 − 5 ! 1 + 6 ! 1 − 7 ! 1 + ⋯
= e − 1
Since e − 1 = 1 − 1 ! 1 + 2 ! 1 − 3 ! 1 + 4 ! 1 − 5 ! 1 + 6 ! 1 − 7 ! 1 + ⋯
Same as Evaluting the denominator as
1 ! 2 + 3 ! 4 + 5 ! 6 + ⋯
1 ! 1 + 1 + 3 ! 3 + 1 + 5 ! 5 + 1 + ⋯
1 + 1 ! 1 + 2 ! 1 + 3 ! 1 + 4 ! 1 + 5 ! 1 + 6 ! 1 + ⋯
= e
Therefore,
e e − 1 = e 2 1