Some algebra, some geometry, and an incenter

Geometry Level 2

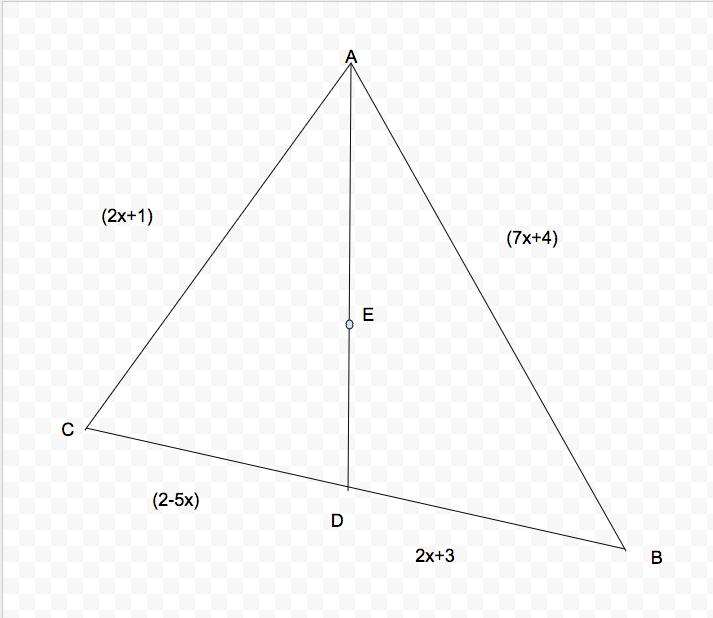
In the figure below, $ABC$ , $ABD$ , and $ADC$ are triangles. $E$ is the incenter of triangle $ABC$ , and it lies on line segment $AD$ .

Find the length of line segment $AD$ . Round your answer to 2 decimal places. A scientific calculator is allowed.

Note: The diagram is NOT to scale.

3.13 2.87 2.22 1.74

1 solution

Yashas Ravi
Mar 14, 2018

Since $E$ is the incenter, and it lies on line segment $AD$ , $AD$ is an angle bisector because the incenter is the point where the $3$ angle bisectors of a triangle meet.
Use the angle bisector theorem to solve for $x$ : $\frac{7x+4}{2x+3}$ $=$ $\frac{2x+1}{2-5x}$ .
After solving for $x$ , substitute the value of $x$ into each expression to find the side lengths.
Use the law of cosines to find the measure of angle $B$ ; $AC^2 = AB^2 + BC^2 - 2(AB)(BC)\cos (B)$ .
After determining the value of angle $B$ , use the law of cosines again to find the length of line segment $AD$ ; $AD^2 = AB^2 + BD^2 - 2(AB)(BD) \cos(B)$ .
The answer you get from this should be $2.22$ . If you did not, you either did not perform the right steps or made an arithmetic error when performing an arithmetic operation (adding/subtracting/multiplying/dividing).