Some grid
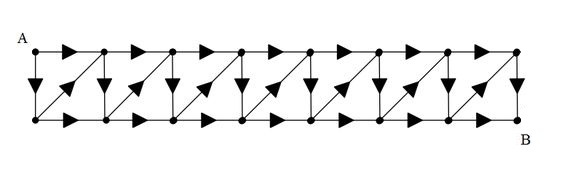
The diagram above shows a tiling of 7 squares with A and B denoting the initial point and destination point, respectively. The arrow signs indicate the direction that you're able to travel to (east, south, north-east). Find the total number of ways to reach point B from point A .
Bonus : Generalize this for n squares.
The answer is 987.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Moderator note:
Great image! That's a common first approach to solving these kind of "get from A to B" problems.
I couldn't solve without the clue :D
had a calculation mistake...
Here's a different approach and different formula.
Suppose you are taking k diagonal steps, then your path length is n + k + 1 . The important point to note is each diagonal step must precede exactly 1 down step and succeed exactly 1 down step. Therefore there is total 2 × k + 1 down and diagonal steps.
Let us name the steps as follows
- R - Right step
- D - Down step
- Di - Diagonal step
Suppose we are taking 1 diagonal step, then we can represent this as
P D Q Di R D S
. Where
P
,
Q
,
R
and
S
are zero or more right steps.
If we will take k diagonal steps then the order of down and diagonal steps is always the same. Therefore we just need to find how many ways we can place the diagonal and down steps in n + k + 1 places. And the remaining empty spaces can be filled by right steps.
∴ Total number of ways to reach to the lower right corner from the upper left corner in n square figure = ∑ k = 0 n ( 2 k + 1 n + 1 + k )
Wonderful work!
As a bonus: Can you prove that the final sum is always a Fibonacci number?
To compute quickly the general formula F 2 n + 2 , use F k ≈ 5 ϕ k with ϕ = 2 1 + 5 .
Here, it gives 3 . 0 7 , 8 . 0 2 , 2 1 . 0 1 , ⋯ and F 2 ⋅ 7 + 2 ≈ 9 8 7 . 0 0 0 2 .
THANK YOU FOR YOUR SOLUTION!
Define f ( n ) to be the number of paths from the top-left corner to the bottom-right corner in a grid of n squares. Note that f ( 0 ) = F 2 = 1 , f ( 1 ) = F 4 = 3 , and so we argue that f ( n ) = F 2 n + 2 , where F n is the n th Fibonacci number 1 , 1 , 2 , 3 , … .
Now, we can see that F 2 n + 2 − 2 F 2 n = F 2 n − 1 = F 2 n − F 2 n − 2 , so it is sufficient to show that f ( n ) − 2 f ( n − 1 ) = f ( n − 1 ) − f ( n − 2 ) . So we show that the two sides count the same number of paths.
Both count the paths that avoid the vertex C to the right of A . The left-hand side starts with all paths and removes the two subcases that go through C . The right-hand side is the number of paths starting at C and moving down in the first step, which is equivalent to the number of paths starting at the vertex below C , which in turn is equivalent to the number of paths that avoid C .
A n = F 2 n + 3 , where F n is the n t h Fibonacci number in the sequence: ( 0 , 1 , 1 , 2 , 3 , 5 , . . . )
Moderator note:
Can you elaborate on it? How did you arrive to that conclusion?
I hate myself for inputting 983 .... damn calculation errors !!!
@Pi Han Goh Great problem; I didn't initially anticipate Fibonacci popping up, so that was a nice surprise. :)
Just wondering what would happen if we had a second such grid stacked above the first one, and then looked for the number of paths from the upper left corner to the lower right corner. Could be messy, but there is a chance for a nice result such as is the case here.
Log in to reply
I'm already working on that a few days ago, I can't spot a pattern here, maybe some programming code would help! ;)
shouldn't the answer be 2584?
Log in to reply
Nevermind I must be drunk. I swore the question said 8 grids
Log in to reply
It did; the problem was changed shortly after. (Originally it said 7 squares but the picture had 8 squares, then the modification made the problem incorrect with both saying 8 squares. Now it's the correct one with 7 squares.)
Generalization for n squares (recognized from the pattern) -
f ( n ) = F 2 n + 2
where F n is n t h number in Fibonacci Series.