Some Nice Dynamics
Let x be a function of time, such that the following are satisfied:
x ¨ + x 2 + x ˙ − 3 = 0 x ( 0 ) = 0 x ˙ ( 0 ) = 0
What is the maximum value of x over time?
The answer is 2.2451.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
I used Laplace transform and I got a maximum value of 2.643.
Log in to reply
The Laplace transform is generally used to solve linear differential equations. While there is a formula for the Laplace transform of x 2 as a type of autoconvolution of the Laplace transform of x with itself, I am not sure how you intend to use this result. My answer (and I guess, Steven's) comes from simple numerical integration of the differential equation.
I don't think there's a simple closed form that you can get with a Laplace transform or any other symbolic method- numerics are required.
Thanks for the clarification. @Mark Hennings. I misread x^2 as t^2.
Here's the phase flow represented by vector field V ( x , y ) = ( y , 3 − y − x 2 ) . I think it looks pretty cool.
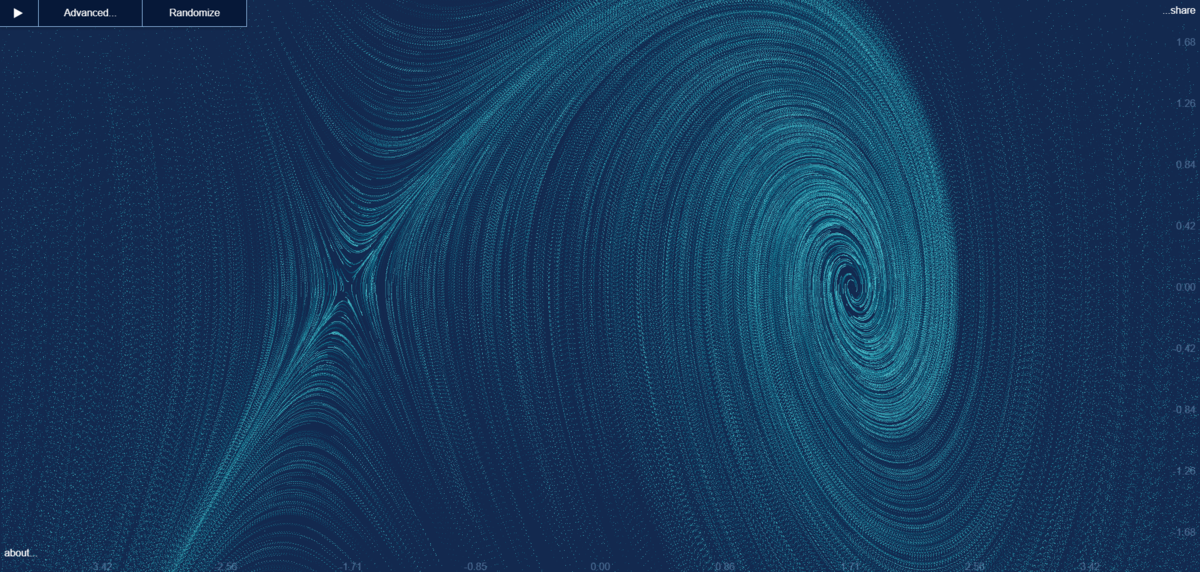
Here's the link if someone wants to play - Field play .
Log in to reply
That looks really cool
Man I tried it myself and it was so amazing! GLSL really is powerful. 1000000 particles; my GPU had no problem and it looked so beautiful!
Although this is a nonlinear equation, it models a particle of mass 1 that is subject to a force 3 − x 2 (which is always directed towards the value x = 3 ) and a further damping force − x ˙ . Thus it is clear that the particle will (eventually) settle down to the equilibrium position of x = 3 . Since we are asked for a maximum value, and not a supremum value, the first swing of the oscillation must take the particle from x = 0 to beyond x = 3 , and the maximum value of x will then be obtained as the maximum value of x during this first swing.
Numerical integration tells us that the maximum value occurs at t = 2 . 1 0 3 7 3 , and is 2 . 2 4 5 1 3 .