Some secondary parts of a triangle II
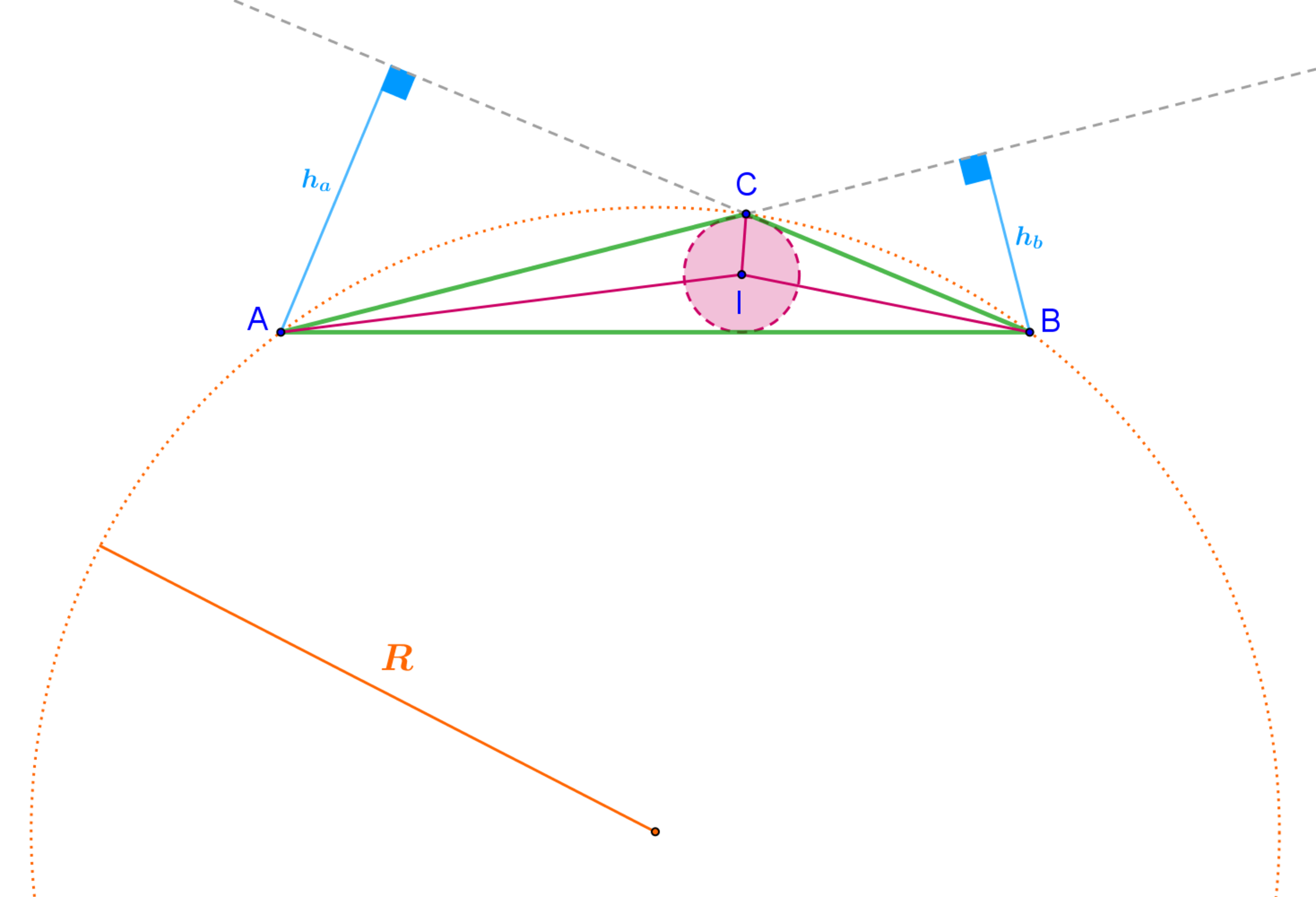 About triangle
A
B
C
we know that:
About triangle
A
B
C
we know that:
- h a = 4 8
- h b = 7 5
- I A ⋅ I B ⋅ I C = 9 0 0 R
Where h a , h b are the altitudes to sides a = B C and b = C A respectively, I is the incenter and R is the circumradius of the triangle.
Find its perimeter.
The answer is 400.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Nice alternative!
But Heron's Rule is a consequence of the Cosine Rule, since cos C = 2 a b a 2 + b 2 − c 2 gives sin C = a b 2 s ( s − a ) ( s − b ) ( s − c ) by simple algebra, and hence Δ = 2 1 a b sin C = s ( s − a ) ( s − b ) ( s − c ) . Thus you are simply following through the details of the proof of Heron's Formula.
Let r be the inradius and s the semiperimeter of the triangle. Denote A B by c .
For this solution, we use some properties of the incenter one can find here and the result Mark Hennings proved in his solution to this problem.
Precisely, we need the formulae I A ⋅ I B ⋅ I C = 4 R r 2 h a 1 + h b 1 + h c 1 = r 1 Heron’s formula: [ A B C ] = s ( s − a ) ( s − b ) ( s − c ) ( 1 ) ( 2 ) ( 3 ) Step 1 : the inradius ( 1 ) ⇒ 9 0 0 R = 4 R r 2 ⇒ r 2 = 2 2 5 ⇒ r = 1 5 Step 2 : the third altitude: ( 2 ) ⇒ 4 8 1 + 7 5 1 + h c 1 = 1 5 1 ⇒ h c = 1 3 4 0 0 Step 3 : the triangle’s sides [ A B C ] = 2 1 h a ⋅ a = 2 1 h b ⋅ b = 2 1 h c ⋅ c ⇒ 4 8 a = 7 5 b = 1 3 4 0 0 c ⇒ ⎩ ⎨ ⎧ b = 2 5 1 6 a c = 2 5 3 9 a
s = 2 a + b + c = ( 1 + 2 5 1 6 + 2 5 3 9 ) 2 a ⇒ s = 2 5 4 0 a
s − a = 2 5 4 0 a − a = 2 5 1 5 a s − b = 2 5 4 0 a − 2 5 1 6 a = 2 5 2 4 a s − c = 2 5 4 0 a − 2 5 3 9 a = 2 5 1 a
Now, Heron’s formula
(
3
)
⇒
(
2
1
h
a
a
)
2
=
2
5
4
0
⋅
2
5
1
5
⋅
2
5
2
4
⋅
2
5
1
⋅
a
4
⇒
2
4
2
a
2
=
2
5
4
1
4
4
0
0
a
4
⇒
a
2
=
1
2
0
2
2
4
2
⋅
2
5
4
⇒
a
=
1
2
5
Consequently,
b
=
2
5
1
6
⋅
1
2
5
⇒
b
=
8
0
c
=
2
5
3
9
⋅
1
2
5
⇒
c
=
1
9
5
For the answer, the perimeter is
a
+
b
+
c
=
1
2
5
+
8
0
+
1
9
5
=
4
0
0
The proof of (1) is easy.We note that s − a = I A cos 2 1 A = I A b c s ( s − a ) so that I A = s ( s − a ) b c and similarly for I B , I C , so that I A ⋅ I B ⋅ I C = s 3 ( s − a ) ( s − b ) ( s − c ) a b c = s 2 Δ a b c = s 2 4 R Δ 2 = 4 R r 2
By the properties of an incenter , I A ⋅ I B ⋅ I C = 4 R r 2 = 9 0 0 R , which solves to r = 1 5 .
The area of a triangle is T = r s , so T = 1 5 s .
The area of a triangle is also T = 2 1 b h , so 2 T = 4 8 a and 2 T = 7 5 b .
By Heron's formula the area of a triangle is also T 2 = s ( s − a ) ( s − b ) ( s − c ) , where 2 s = a + b + c .
These five equations solve to positive solutions of a = 1 2 5 , b = 8 0 , c = 1 9 5 , s = 2 0 0 , and T = 3 0 0 0 .
Therefore, the perimeter is 2 s = 2 ⋅ 2 0 0 = 4 0 0 .
Great! Thanks for contributing!
We can solve this without using Heron's formula .
We have I A ⋅ I B ⋅ I C = 4 R r 2 ( see [9] ), where R and r are the circumradius and inradius of △ A B C respectively. Then we have 4 R r 2 = 9 0 0 R , ⟹ r = 1 5 .
We also have r 1 = h a 1 + h b 1 + h c 1 ( see [12] ) ⟹ 1 5 1 = 4 8 1 + 7 5 1 + h c 1 ⟹ h c = 1 3 4 0 0 .
Since the area of △ A B C , [ A B C ] = 2 a h a = 2 b h b = 2 c h c ⟹ a : b : c = 4 8 1 : 7 5 1 : 4 0 0 1 3 = 2 5 : 1 6 : 3 9 . Then by cosine rule we have 3 9 2 = 2 5 2 + 1 6 2 − 2 ( 2 5 ) ( 1 6 ) cos C , ⟹ cos C = − 0 . 8 ⟹ sin C = 0 . 6 .
The area of △ A B C is also given by [ A B C ] = 2 a b sin C = 2 a h a , ⟹ 0 . 6 b = 4 8 ⟹ b = 8 0 ⟹ a = 1 2 5 and c = 1 9 5 and the perimeter a + b + c = 1 2 5 + 8 0 + 1 9 5 = 4 0 0 .