A focused parabola
Consider the parabola with minimum point at the origin and focus one unit above.
I draw a line of length 1 0 1 units from the focus to the the point on the parabola in the first quadrant ( x 0 , y 0 ) .
Find the gradient of the tangent at x = x 0 .
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
The parabola is described by y = x 2 / 4 , which can easily be derived.
There is a property of parabolas: a parabola can be defined as the locus of points which are equidistant from a focus as well as a directrix. Using this, we then know that y 0 = 1 0 0 , since the directrix is y dir = − 1 . Hence, we get that x 0 = 2 0 .
Now, to find the tangent, we simply differentiate:
d x d y ∣ ∣ ∣ ∣ x = x 0 = x 0 / 2 = 1 0
For a parabola of the form y = a ( x − h ) 2 + k , the critical point is located at the co-ordinates ( h , k ) , and the focus is located at ( h , k + 4 a 1 ) .
Given that the minimum of the parabola is at ( 0 , 1 ) , and the minimum — which is a type of critical point — is located at ( 0 , 0 ) . Therefore, h = k = 0 So 4 a 1 = 1 a = 4 1
Therefore the equation of the parabola is
y
=
4
1
x
2
. Differentiating, we get
d
x
d
y
=
4
1
(
2
)
x
2
−
1
=
2
1
x
.
We'll need this to find the gradient described in the problem.
A line of length 1 0 1 units is drawn from the focus to the point ( x 0 , y 0 ) on the parabola. Given that ( x 0 , y 0 ) lies in the first quadrant, find the gradient of the tangent at x = x 0 .
The first thing we want to find is (effectively) the point of intersection between the parabola, and the circle with centre ( 0 , 1 ) and radius 1 0 1 . So, we have ( x − 0 ) 2 + ( y − 1 ) 2 = 1 0 1 2 . Substituting in for y , x 2 + ( 4 x 2 ) 2 = 1 0 1 2 x 2 + [ 1 6 x 4 − 2 ( 4 x 2 ) + 1 ] = 1 0 2 0 1 2 x 2 + 1 6 x 4 = 1 0 2 0 0 x 4 + 8 x 2 = 1 6 3 2 0 0 Let z = x 2 . So z 2 + 8 z = 1 6 3 2 0 0 Therefore, ( z + 4 ) 2 = ( 4 ) 2 + 1 6 3 2 0 0 ( z + 4 ) 2 = 1 6 3 2 1 6 z + 4 = ± 1 6 3 2 1 6 = ± 4 0 4 z = − 4 ± 4 0 4 Ignore negative solution, as x 2 is real. Therfore z = 4 0 0 Substituting in for z , x 2 = 4 0 0 x = ± 4 0 0 = ± 2 0 However, x 0 is in the first quadrant, making it positive. So x 0 = 2 0
All that is left to do is to find the tangent at x = 2 0 . Plugging in this value for the formula for the derivative, we acquire 2 1 ( 2 0 ) = 1 0 ,
yielding our final answer.
I came up with a solution that doesn't require knowledge of the formula(s) for the focus: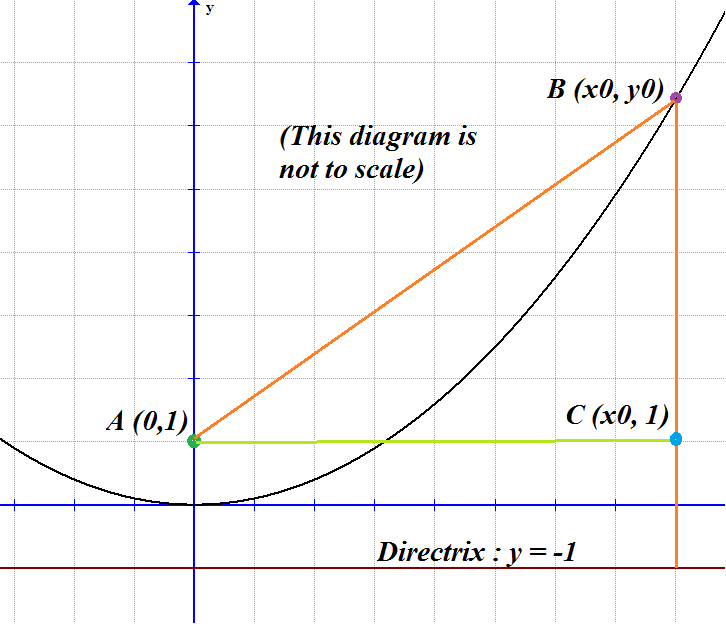
Let A be the focus, O be the origin and B the point ( x 0 , y 0 ) . Since the minimum point is the origin, the equation must be of the form y = a x 2 .
Now each point on the parabola is equidistant from the focus and directrix. Since O is a distance of 1 from the focus, therefore the directrix must be y = − 1 .
It is also known that B is 1 0 1 units away from the focus. Hence it is also 1 0 1 units from the directrix (i.e. the two orange lines in the diagram are of equal length). Thus y 0 = − 1 + 1 0 1 = 1 0 0 .
Let C be the point ( x 0 , 1 ) as in the diagram. Then, in the triangle A B C we have B C = 9 9 , A B = 1 0 1 and ∠ A C B = 9 0 ∘ . Therefore, by the Pythagorean Theorem, A C = 1 0 1 2 − 9 9 2 = 2 0 .
Thus x 0 = 2 0 and y 0 = 1 0 0 . Since y 0 = a x 0 2 , this gives us a = 4 1 . Hence the parabola is y = 4 1 x 2 . The derivative of the parabola is 2 x , so when x = 2 0 the slope of the tangent is 1 0 .