Something Similar To Fibonacci Squares
1 2 + 1 2 + 1 2 + 3 2 + 4 2 + 7 2 + 1 1 2 = ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
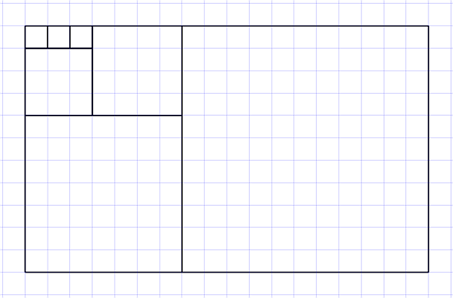
If you look at the squares from the top left, you will notice that we have
3 1X1 squares,
1 3X3 square,
1 4X4 square,
1 7X7 square,
1 11X11 square.
Hence, the area of the rectangle is 1 2 + 1 2 + 1 2 + 3 2 + 4 2 + 7 2 + 1 1 2 .
We can also calculate the area of the rectangle directly. Since it has a height of 11, and a width of 18, hence it has an area of 1 1 × 1 8 = 1 9 8 .
Thus, the area of the rectangle is 1 2 + 1 2 + 1 2 + 3 2 + 4 2 + 7 2 + 1 1 2 = 1 9 8 .
Unfortunately the final 11 squared was missing on my display, so I could not be certain what I was solving for.
Log in to reply
Can you send me a screenshot of what you saw? There should be a scrol bar to indicate that the Latex equation is incomplete.
You can email me: Calvin at Brilliant.org
And as an added easy way to multiply by 11. Take sum of first and second digit and place it in between the digits. 18x11 is 1(1+8)8 = 198.
Brilliant! But try 57. Does weird stuff. 5(5+7)7 is... [5(1],2)7...(brackets mine cuz they become the 6 in 627?). So is that a repeatable pattern if the two added numbers in parentheses equal double digits? Far left ones get added? (Like the two in my brackets?) 6(6+7)7 or [6(1]3)7or 737...huh... neato.
1 2 + 1 2 + 1 2 + 3 2 + 4 2 + 7 2 + 1 1 2 = 1 + 1 + 1 + 9 + 1 6 + 4 9 + 1 2 1 = 1 9 8
You can see that the rectangle formed by the square with a side length of 11. 198 is the only number that is a multiple of 11. You can do the same for the 18, which has a factor of 3. 198 is the only multiple of 3 ( 1 + 9 + 8 = 1 8 1 + 8 = 9 ) .
the hard way: count the squares
the easy way: 1 1 ∗ 1 8 do the math
Find out the area, which is 11 x 18
Find the area of the square given in the diagram.
Its length is 1 1 + 7 = 1 8 units and breadth is 7 + 4 = 1 1 units.
So, the answer is length × breadth = 1 8 × 1 1 = 1 9 8 sq.units.
Alternatively,
Addition = ( 1 + 1 + 1 + 9 + 1 6 + 4 9 + 1 2 1 = 1 9 8 )