Sophisticated Timers
Alan has two identical timers, which both have a preset amount of seconds that tick down to 0.
These sophisticated timers have a weird property, when the number of seconds left on the timer is a multiple of 10, it makes a squeaking sound, and when the number of seconds left on the timer is a multiple of 30, it makes a barking sound.
Alan started both timers at the same time , and after both timers have reached 0, he makes the following statements:
(1) The second squeak can be heard 3 seconds after the first squeak .
(2) The last squeak can be heard 7 seconds after the second-to-last squeak .
(3) I heard a total number of 6 barks .
(4) At the time both timer started, there was a 21 second delay before the 2nd bark can be heard.
Let and be the initial preset amount of seconds on both timers. What is ?
Details and assumptions:
-
As 30 is also a multiple of 10, when the number of seconds left on the timer is a multiple of 30, it will simultaneously squeak and bark
-
is a multiple of 10 as well as a multiple of 30
-
Alan has perfect hearing
-
Alan has a perfect sense of time
-
No actual dogs or mice are involved
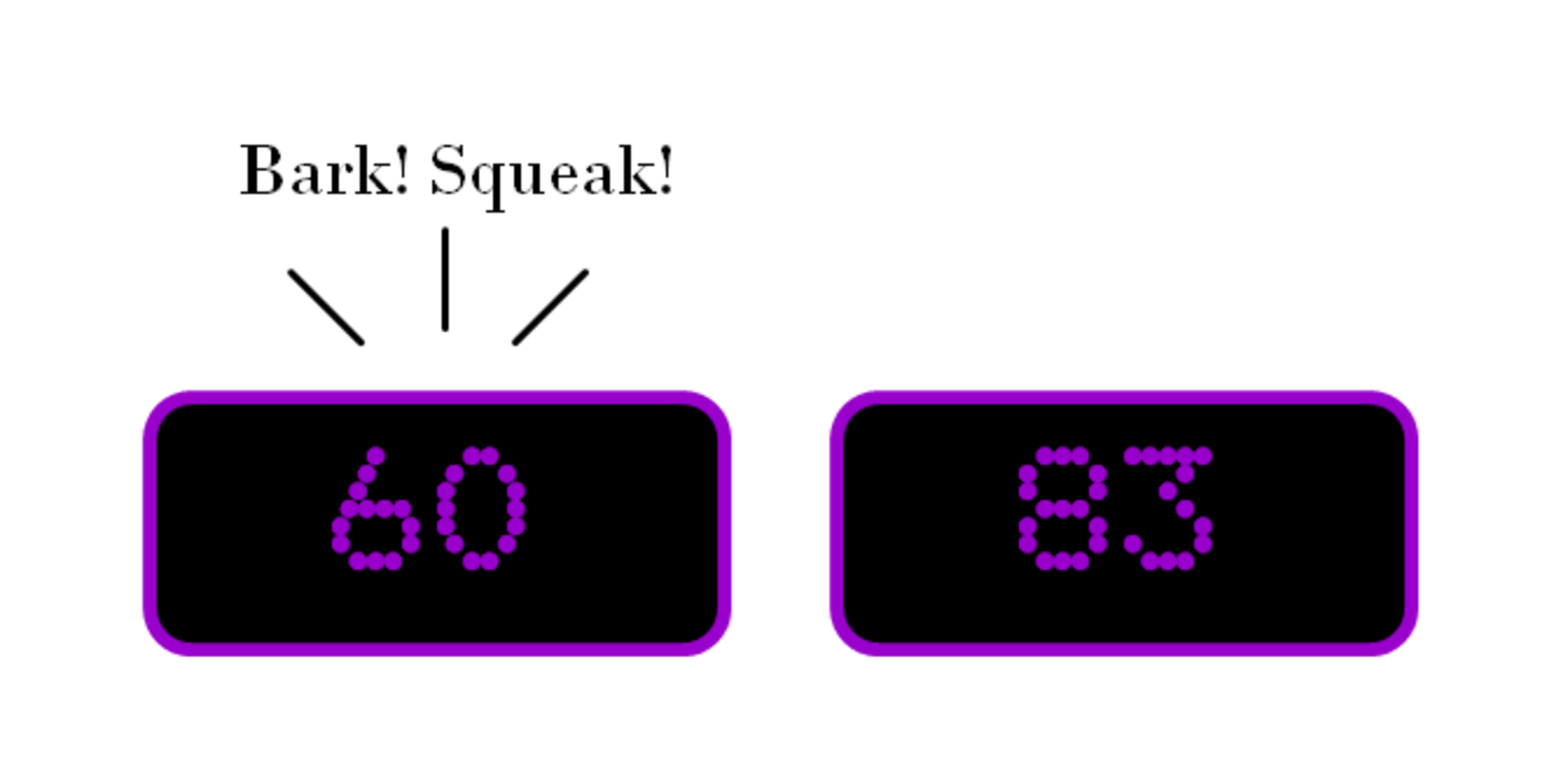
The answer is 155.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We call the two timers TA and TB, based on their initial presets; and, WLOG, suppose A > B. From (2), we know that A = B + 7; this also means that the TA will bark at most one time more than TB (for TA to bark two more times than TB, we would need A > B + 30). But from (3) the total number off barks is even; so TA and TB must bark the same number of times, i.e. three times each. These barks must occur with 0, 30 and 60 seconds left on the timers, thus 60 < A, B < 90. Finally, since both timers bark the same number of times and A > B, the second bark must be A's, and it must happen with 60 seconds remaining; therefore from (4) it had to start with 60 + 21 = 81 seconds, and then B had to start with 81 - 7 = 74 seconds. So our answer is A + B = 81 + 74 = 1 5 5
It would seem (unless I missed something!) that clue (1) was unnecessary.