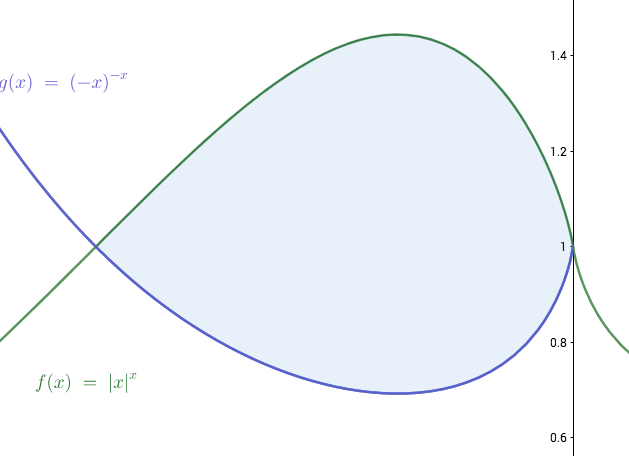
Sophomore's Leaf

We can make $x = -x$ and take the positive side, for simplicty. The intersection points will be $0$ and $1$ and, since $x$ is positive, $|x| = x$ . Thus, this becomes:

$\large \displaystyle A = \int_0^1 (x^{-x} - x^x) dx$

$\large \displaystyle A = \int_0^1 e^{-x \ln(x)}dx - \int_0^1 e^{x \ln(x)}dx$

$\large \displaystyle A = \int_0^1 \sum_{k=0}^{\infty} \frac{1}{k!} [-x \ln(x)]^k dx - \int_0^1 \sum_{k=0}^{\infty} \frac{1}{k!} [x \ln(x)]^k dx$

$\large \displaystyle A = \sum_{k=0}^{\infty} \frac{1}{k!} \left [ \int_0^1 [-x \ln(x)]^k dx - \int_0^1 [x \ln(x)]^k dx \right ]$

Make $u = -\ln(x)$ on both integrals. Then, $x = e^{-u}$ and $dx = -e^{-u} du$ :

$\large \displaystyle A = \sum_{k=0}^{\infty} \frac{1}{k!} \left [ \int_0^{\infty} e^{-u(k+1)} u^k du - (-1)^k \int_0^{\infty} e^{-u(k+1)} u^k du \right ]$

$\large \displaystyle A = \sum_{k=0}^{\infty} \frac{1 - (-1)^k}{k!} \left [ \int_0^{\infty} e^{-u(k+1)} u^k du \right ]$

Multuply above and below by $(k+1)^k$ :

$\large \displaystyle A = \sum_{k=0}^{\infty} \frac{1 - (-1)^k}{k! (k+1)^k} \left [ \int_0^{\infty} e^{-u(k+1)} [u(k+1)]^k du \right ]$

Make $t = u(k+1)$ . Then, $dt = du (k+1)$ :

$\large \displaystyle A = \sum_{k=0}^{\infty} \frac{1 - (-1)^k}{k! (k+1)^k} \cdot \frac{1}{k+1} \left [ \int_0^{\infty} e^{-t} t^k dt \right ]$

The integral is the exact definiton of $\Gamma(k+1)$ , which is equal to $k!$ :

$\large \displaystyle A = \sum_{k=0}^{\infty} \frac{1 - (-1)^k}{k! (k+1)^{k+1}} \cdot k!$

$\large \displaystyle A = \sum_{k=0}^{\infty} \frac{1 - (-1)^k}{(k+1)^{k+1}}$

Make $n = k+1$ :

$\large \displaystyle A = \sum_{n=1}^{\infty} \frac{1 - (-1)^{n-1}}{n^n}$

The numerator will be $0$ for odd $n$ and $2$ for even $n$ . Thus:

$\large \displaystyle A = \sum_{n=1}^{\infty} \frac{2}{(2n)^{2n}}$

This sum quickly converges ( $5$ steps) to:

$\color{#20A900} \boxed{ \large \displaystyle A = 0.507855486}$

Correct to $9$ decimal places. Thus:

$\color{#3D99F6} \boxed{ \large \displaystyle \lfloor A \rfloor = 50785}$