Sorted triangles
How many ways can you put all the numbers 1 through 9 in this triangular grid, such that numbers along each arrow form an increasing sequence?
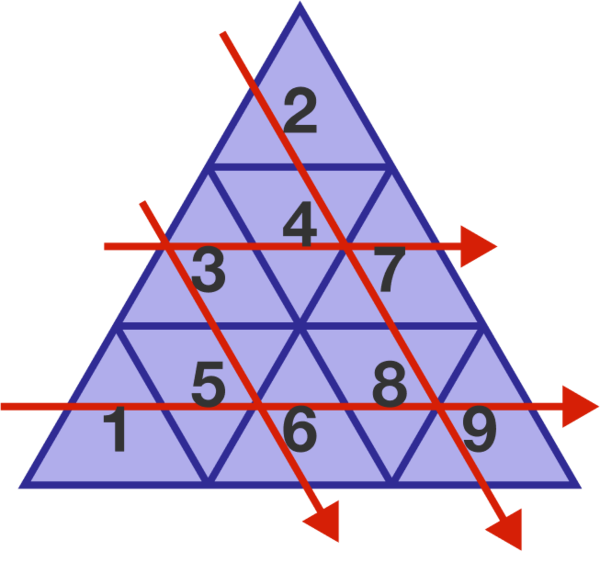
The diagram shows one possible configuration.
The answer is 52.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
10 solutions
Is there any precise solution to this problem? i wanna to find a quicker way because I calculate the problem from the bottom-right number and take kind of complex process to get the answer.
Hey man so could you give me the formula in which you learned how to do this equation for I'm a junior in high school and I'm spending 100$ a year for this so I'm getting my money's worth
Log in to reply
I wish I had a cool formula, like the hook formula, but the diagram above is the best I got... :-/
I like your reasoning, Dong! Almost hints at a general solution for n triangles!
Wow, that's exactly how I did it.
For ease of explaining, I'll be turning the triangle upright, so the largest number is at the bottom, and the smallest five numbers are on the top row.
As 9 is the largest number, it cannot go above another number. This places it in the bottom triangle. Similarly, 8 must go in the triangle directly above that, otherwise it would be above a smaller number.
The number 7 must go adjacent to the 8 . If it is in the top row, it will again be above a smaller number.
The other number adjacent to the
8
cannot be less than
4
, as there are three numbers above it, and thus three numbers smaller than it. This means we can work out the number of possible solutions for
4
,
5
&
6
in this position, and then double it to find the solution (as it and the
7
can swap places).
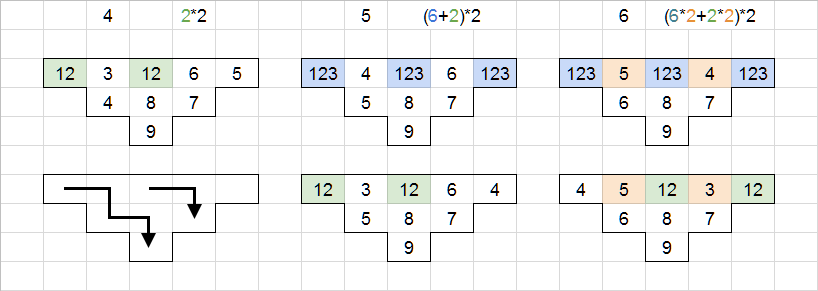 For
4
: The numbers
6
and
5
are forced to be above
7
, as they are both greater than
4
. This leaves
3
to be directly above
4
, and
1
&
2
interchangeable between the remaining two triangles. This gives us
2
possible solutions for
4
.
For
4
: The numbers
6
and
5
are forced to be above
7
, as they are both greater than
4
. This leaves
3
to be directly above
4
, and
1
&
2
interchangeable between the remaining two triangles. This gives us
2
possible solutions for
4
.
For 5 : The number 6 must be above 7 , and either 3 or 4 above 5 . In the former case, 1 , 2 & 3 can be in any of the remaining triangles. In the latter case, 4 must be above 6 , leaving the 1 & 2 in either of the remaining triangles. This gives us 6 + 2 possible solutions for 5 .
For 6 : The number 5 must be above the 6 or 7 , and the other must be either 3 or 4 . Similar to the previous one, the free numbers are 1 , 2 & 3 and 1 & 2 respectively. However, as the two larger numbers in the top row are also interchangeable, this doubles the number of possible solutions for 6 , at 6 × 2 + 2 × 2 .
Adding these up, and doubling them to account for the 7 position gives us ( 2 + 6 + 2 + 6 × 2 + 2 × 2 ) × 2 = 5 2 .
Apologies for the square triangles. It was neater just using sheets than actually trying to draw the triangles myself.
Pink ideas
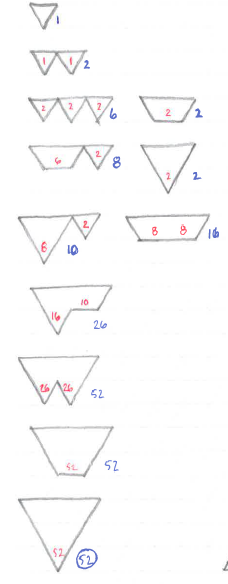
I worked top down instead of bottom up. (I also rotated 60 degrees.)
The blue number for each shape is the number of ways of numbering that shape. The red numbers inside are the blue numbers that come from the previous level. (I'm noticing the light grey background grid of triangles is really hard to see in this scan.)
This method allowed me to solve the next larger triangle (1 to 16) which I intend to submit as a follow-up to this.
**Mathematica
Length@Select[Permutations@Range@9, And @@ OrderedQ /@ {#[[{1, 3, 4, 8, 9}]], #[[{2, 6, 7}]], #[[{2, 3, 4}]], #[[{5, 6, 7, 8, 9}]]} &]
returns 52
Who doesn't like a quick and dirty brute force?
import itertools
print(len(list(filter(lambda L: L[0] < L[2] < L[3] < L[7] < L[8] and L[1] < L[5] and L[1] < L[2] and L[4] < L[5] < L[6] < L[7], itertools.permutations(range(9))))))
This will recursively iterate through all possible formations and test if each arrow has an increasing sequence. It runs surprisingly quickly in the code runner as well. Each section in the triangle grid was assigned an index according to the table below, which was used to determine valid solutions.
| 0 | ||||
| 1 | 2 | 3 | ||
| 4 | 5 | 6 | 7 | 8 |
when i feel clueless i tend to do brute force too, then start making progress once i know the answer, or an aproximation
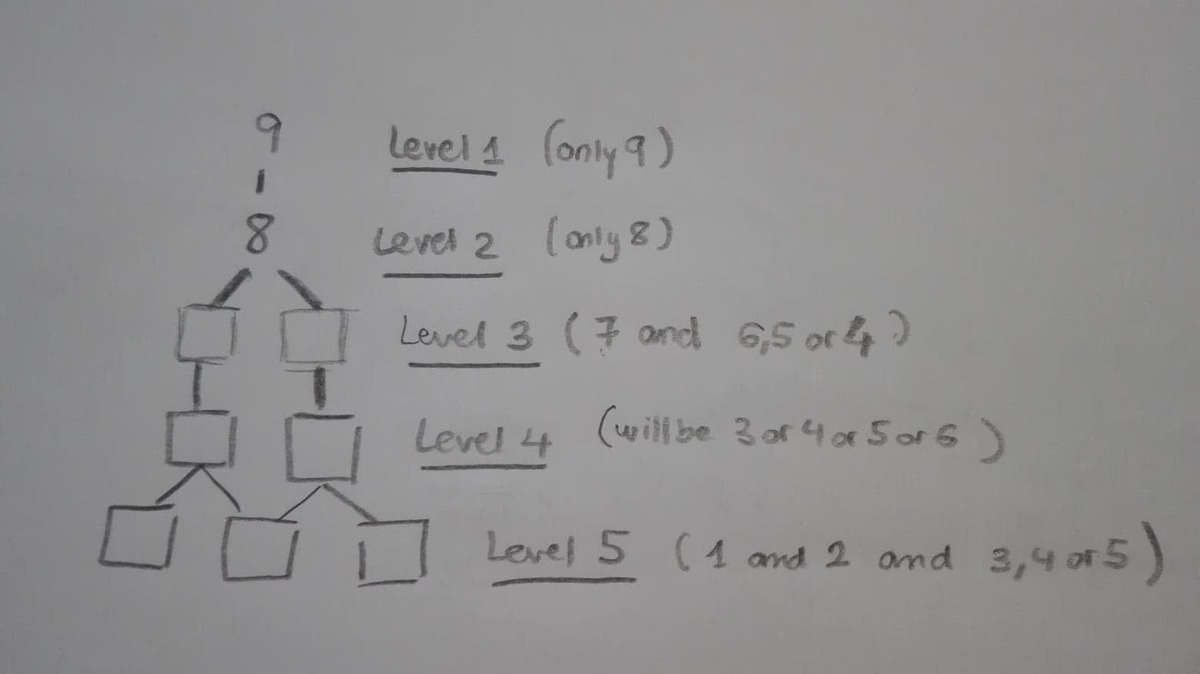
Level 3 can be only combinations of 7 with 4, 5, or 6.
When level 3 is 7 and 4 (2 ways) -> level 4 can contain only 6 and 3 fixed below 7 and 4 respectively (still 2 ways) -> so level 5 must have 5 fixed below 6, only 1 and 2 can permutate. so 2x2 = 4 ways.
When level 3 is
7 and 5
(2 ways)
-> level 4 must have 6 fixed below 7, and 3 or 4 below 5 (2x2 = 4 ways now)
-> level 5 : if level 4 had 6 and 4, then all permutations of 123 (2x6 ways). If level 4 was 6 and 3, then 4 is fixed below 6 so only 1 and 2 permutate (2x2 ways). So 2x2 + 2x6 = 16 ways.
When level 3 is 7 and 6 (2 ways) -> level 4 must contain 5 and the other number will be 3 or 4, so 4 combinations are possible (2x4 = 8 ways now). -> Level 5 :if level 4 has 5 and 4 then all permutations of 123 are possible (4 x 6 ways). If level 4 had 5 and 3 then 4 is fixed below 5 and only 1 and 2 permutate (4 x 2 ways). So 4x6 + 2x4 = 32 ways.
Total: 32 + 16 + 4 = 52.
I did it using Nate Jellis's method from the Sep 17 problems:
They ask for a solution, not how much luck you have by guessing the answer
Redraw as follows, there is a < relationship between adjacent numbers (either in the same or adjacent lane).
| col 1 | col 2 | col 3 | col 4 | col 5 |
| a | ||||
| d | f | |||
| b | 8 | 9 | ||
| e | g | |||
| c |
Observations: - 8 and 9 will always be where they are drawn - 7 has to go into col 3 (either f or g) - b has to be 1,2 or 3, because all numbers except a and c have to be larger than b
A) Set b=3. This forces 1 and 2 into a and c (which can be done in 2 ways). We can independently choose 7 to be at either f or g (again in 2 ways). Having made these two choices, there are 3 posibilities to complete: - 6 before 7 (which settles the rest) - 6 before 8 with 4 before 6 - 6 before 8 with 5 before 6. So, A has 2×2×3=12 possibile arrangements
B) Set b=2. Still, 7 can be at f or g (2 ways). Say it is at f (by symmetry the other case is identical). Now we have two independent paths: ad and ceg. The remaining 5 numbers(1,3,4,5,6) can divided into these paths of length 2 and 3 in 10 ways. Within such a path they can only be in ascending order. Observe that 1 will automatically end up in a or c, so that d and e will automatically be larger than b. So, B has 2×10=20 possible arrangements
C). With b=1 we follow the exact same logic as under B, so also 20 possible arrangements
Together there are 12+20+20=52 possible arrangements.
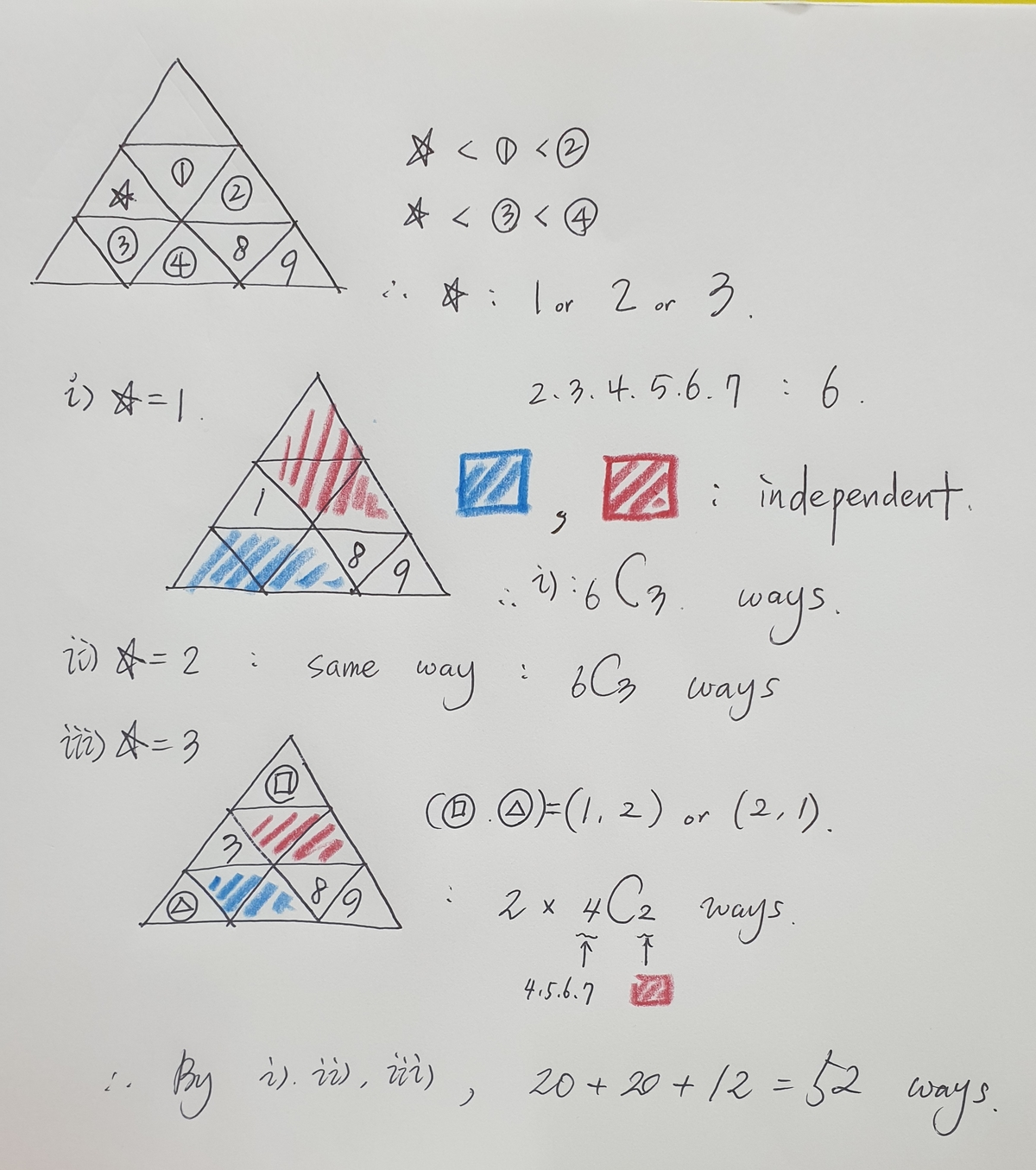
Hows this for a solution?
I'd love to see if anyone came up with a more elegant approach? Perhaps a way to use the hook length formula?