Sorting and then sorting again...
You have the numbers 1 through 9 randomly placed in a grid.
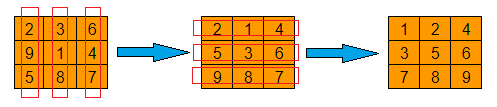
First you sort each element of each column. Then you sort each element of each row.
In the end, is each element of each column necessarily sorted?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
As it turns out, first sorting each column and then sorting each row of a matrix always preserves the sorting by columns. (That is, the 3x3 restraint in the original problem is unnecessary). This can be shown to be true in the following way:
Consider a matrix which has all its columns sorted. Assume that, when starting from the top of the matrix and sorting each successive row, at some point we reach an element which is smaller than the one above it, thus disproving the fact that the columns remain sorted. Now consider the two rows in which the discrepancy occurs. Let their elements respectively be a k and b k for k ∈ [ 1 , n ] . Since the columns were initially sorted, a k < b k . Let’s now begin sorting the two rows anew. Let b i and a j be the smallest elements in their respective rows. If i = j , then those two elements will go to the beginning of the sorted rows and will cause no discrepancy. We can then consider the remainder of the rows over and over until we reach a time where i = j . Since b i > a i > a j , those two elements going to the beginning of the sorted rows will cause no issue. On the other hand, b j > b i > a i , so we can move b j below a i without messing up the column-sort and repeat the argument again until the two rows are sorted. Since both cases preserve the column-sort, our assumption is wrong and the column-sort is always preserved.
Note that this solution assumed the worst-case scenario of having no two elements be equal. This is a worst-case scenario because two elements being equal poses no danger to the column-sort, so in a sense those two elements are given to us “for free”.