Swapping by Powers
You have three urns on a shelf. The left urn contains 16 blue balls, the middle urn has 32 grey balls, and there are 64 red balls in the right urn. Your goal is to re-arrange the contents of the urns so that the contents of the left and right urns are swapped. This might seem simple, but there's a catch: you have to re-arrange by performing special moves. Each move consists of taking some number of balls out of one urn and putting them into another. You must take out a number of balls which is equal to a power of two, and the number of balls in each urn after the move must also be a power of two. What is the minimum number of moves needed to swap the contents of the left and right urns?
Initial Configuration:
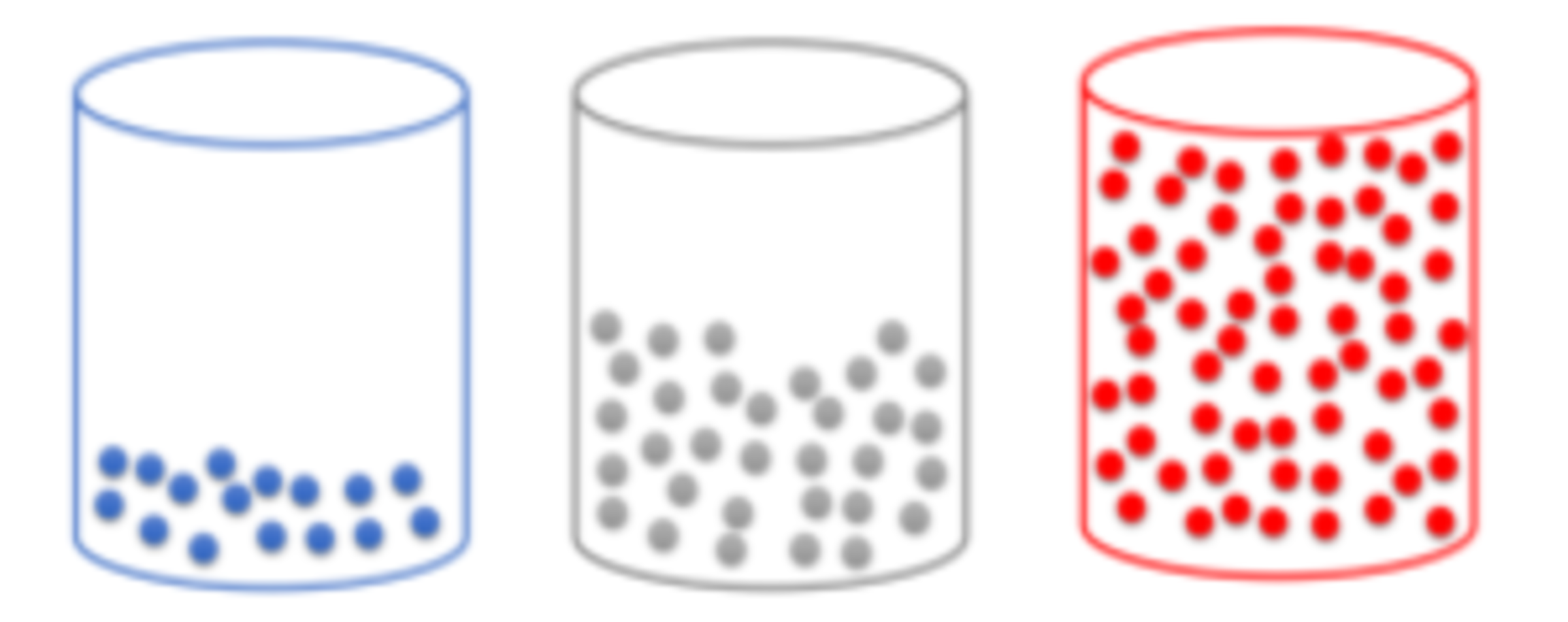
Goal:
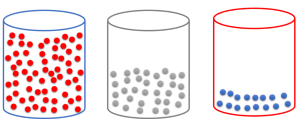
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
There are two possible first moves:
move 16 grey balls from the middle urn to the left urn.
move 32 red balls from the right urn to the middle urn.
If option 1 is taken, these things must happen to complete the swap: move the red balls out of the right urn (no less than 2 moves), move the blue balls from the left urn to the right urn (no less than 1 move), and move the grey balls from the left urn to the middle urn (no less than 1 move). Note that no more than one of these actions can be carried out in one move because no two actions involve transferring between the same urns in the same order. This gives a total of 5 moves minimum.
If option 2 is taken, there are two possibilities for the second move:
move 16 red balls from the right urn to the left urn
move 32 balls (some mixture of red and grey) from the middle urn to the right urn
In the case of second move 1, these things must happen to complete the swap: move the remaining red balls from the right urn to the left urn (no less than 1 move), move the blue balls from the left urn to the right urn (no less than 1 move), and move the red balls that were in the middle urn to the left urn (no less than 1 move). Again, no more than one action can be carried out in a single move. This gives a total of 5 moves minimum.
In the case of second move 2, if the 32 balls moved back to the right were all red, then the situation resets to the start with two moves wasted. Otherwise, these things must happen to complete the swap: move the 32 or more red balls in the right urn out of the right urn (no less than 1 move), move grey balls from the right urn back to the middle urn (no less than 1 move), and move the blue balls from the left urn to the right urn (no less than 1 move). Multiple actions, once again, can't be combined. This gives a total of 5 moves minimum.
The consideration of all the cases above shows that the minimum possible number of moves is five. Here is a way to do it in five moves:
Start: 16 b | 32 g | 64 r
Move 32 red balls from the right to the middle: 16 b | 32 g 32 r | 32 r
Move 16 red balls from the right to the left: 16 b 16 r | 32 g 32 r | 16 r
Move 16 blue balls from the left to the right: 16 r | 32 g 32 r | 16 r 16 b
Move 16 red balls from the right to the left: 32 r | 32 g 32 r | 16 b
Move 32 red balls from the middle to the left: 64 r | 32 g | 16 b