Spaceballs (Part 2)
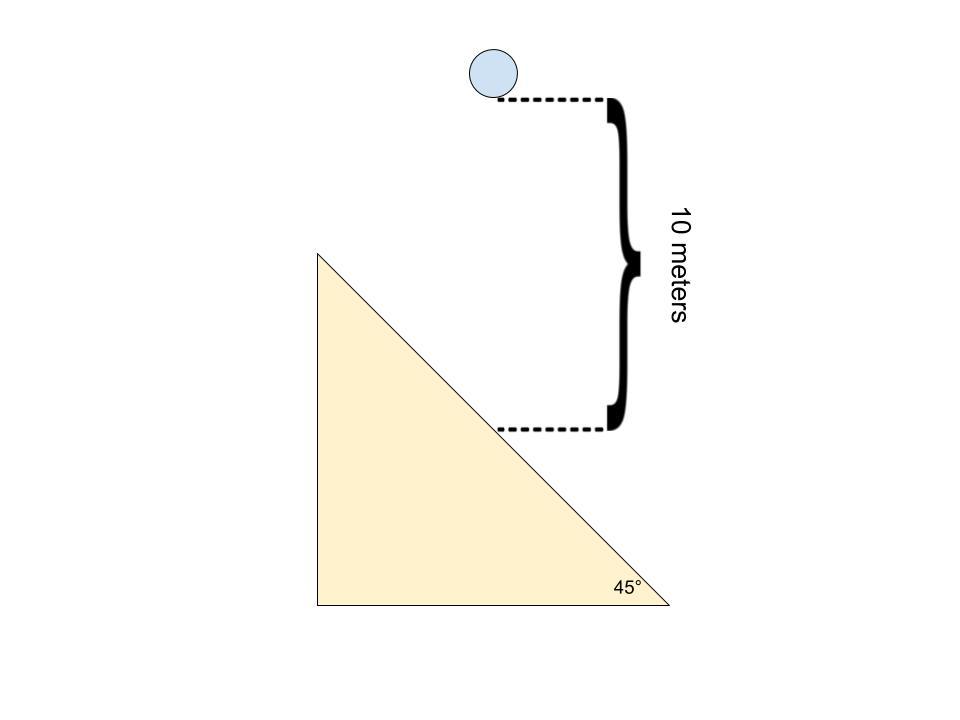
You have two identical setups (shown below) on two separate planets, Earth and Zeta. On Earth, the acceleration due to gravity is ; on Zeta, the acceleration due to gravity is . On each planet, a ball is dropped from rest onto an inclined plank with an angle of elevation of 45° from a height of 10 meters. The balls are allowed to bounce all the way down the planks. How long does it take for the ball on Earth to reach its second bounce (starting from the initial drop)?
Assumptions:
-
The two balls are identical.
-
There is no air resistance.
-
All collisions are perfectly elastic.
-
The planks are long enough for each ball to bounce at least twice.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Refer to Spaceballs (Part 1) to derive the graph that both balls follow on the xy-plane here .
y = 4 0 − x 2
To find how much time the ball spends in the air, we first need to find when it will land again. We do this by defining the plank's position as y = − x on our xy-plane. Now, we need to see when the ball's path will hit the plank.
− x = 4 0 − x 2 x = 4 0 m y = − 4 0 m
Now that we know the ball's x- and y-coordinates when it reaches its second bounce, we can solve for how long it took the ball to travel those distances.
4 0 = 1 4 × t 1 t 1 = 7 2 0 s − 4 0 = 2 − 9 . 8 t 1 2 t 1 = 7 2 0 s
Since we got that it took 7 2 0 s for the ball to reach the plank using both the x- and the y-coordinates, we can be confident that the first part of our answer is correct. The next part is to find out how much time it took for the ball to drop 1 0 m after being released from rest.
− 1 0 = 2 − 9 . 8 t 2 2 t 2 = 7 1 0 s
Finally, we add t 1 and t 2 to get 7 3 0 s .