Spaceballs (Part 1)
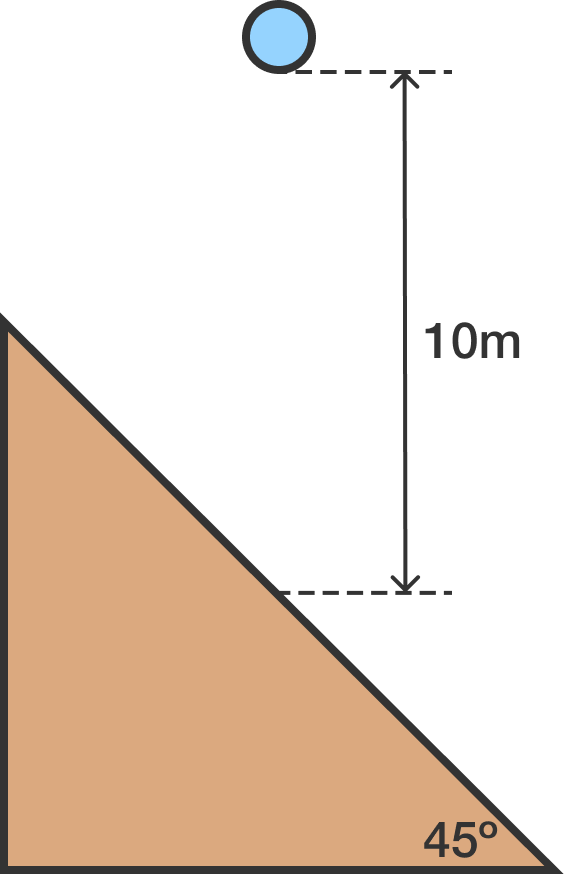 You have two identical setups (shown below) on two separate planets, Earth and Zeta. On Earth, the acceleration due to gravity is
9
.
8
m/s
2
,
while on Zeta the acceleration due to gravity is
7
.
2
m/s
2
.
On each planet, a ball is dropped from rest onto an inclined plank with an angle of elevation of 45° from a height of 10 meters. The balls are allowed to bounce all the way down the planks.
You have two identical setups (shown below) on two separate planets, Earth and Zeta. On Earth, the acceleration due to gravity is
9
.
8
m/s
2
,
while on Zeta the acceleration due to gravity is
7
.
2
m/s
2
.
On each planet, a ball is dropped from rest onto an inclined plank with an angle of elevation of 45° from a height of 10 meters. The balls are allowed to bounce all the way down the planks.
On which planet does the ball spend more time in the air between its first and second bounces?
Assumptions:
- The two balls are identical.
- There is no air resistance.
- All collisions are perfectly elastic.
- The planks are long enough for each ball to bounce at least twice.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Begin this problem by solving for the velocity of each ball the instant before it hits the plank. Do this by using the formula V 2 = V 0 2 + 2 × a × d , where V = Velocity, V 0 = Initial Velocity, a = Acceleration, and d = Distance traveled by the object. On Earth, V 1 2 = 0 2 + 2 ( 9 . 8 s 2 m ) ( 1 0 m ) , so V 1 = 1 4 s m . On Zeta, V 2 2 = 0 2 + 2 ( 7 . 2 s 2 m ) ( 1 0 m ) , so V 2 = 1 2 s m .
Since the plank is tilted at 45°, the balls move exactly horizontally the instant after impact. Also, since the collisions are perfectly elastic, the ball's velocity the instant before impact equals the ball's velocity the instant after impact. This means that on Earth, the ball is moving horizontally with a velocity of 1 4 s m immediately after impact. On Zeta, the ball is moving horizontally with a velocity of 1 2 s m immediately after impact.
These vectors can be visualized by superimposing an xy-plane on top of the picture above with the origin at the impact point. Now, each ball's horizontal distance traveled can be modeled with x = V × t , where t = Time after impact (in seconds). On Earth, x 1 = 1 4 × t . On Zeta, x 2 = 1 2 × t . Each ball's vertical distance traveled can be modeled with y = 2 a t 2 + V 0 t . Each ball is only traveling horizontally the instant after impact, so it's initial downwards velocity is 0 s m . On Earth, y 1 = 2 − 9 . 8 t 2 . On Zeta, y 2 = 2 − 7 . 2 t 2 .
The next step is to combine each ball's horizontal and vertical movement to graph its path on the xy-plane. By solving for t in both of the equations modeling the ball on Earth's movement, you get t = 1 4 x 1 and t = 9 . 8 − 2 y 1 . After setting these two expressions equal to each other and solving for y 1 , you get y 1 = 4 0 − x 1 2 . On Zeta, t = 1 2 x 2 and t = 9 . 8 − 2 y 2 . Combining these expressions, you get y 2 = 4 0 − x 2 2 .
Since both balls follow the same path in the air, the only difference in the time it takes each ball to bounce once more after the initial bounce is the ball's velocity. On Earth, the magnitude of acceleration due to gravity is greater than that of gravity on Zeta, so the ball's speed is greater on Earth than it is on Zeta at every point in its arc relative to that same point on the other ball's arc. Because of this, the ball on Earth covers the distance faster, and the ball on Z e t a spends more time in the air.
To answer the question we do not need to solve the equations of motion. The time of flight will depend on three quantities: the initial height h , the angle of the board α and the acceleration of gravity g . Looking at the units of the quantities we see time (seconds), height (meters), angle (dimensionless for this purpose) and acceleration (m/s 2 ). There is only a single combination that yields the correct unit for the time and that is t = η h / g , where the dimensionless quantity η depends on the angle. Therefore smaller g yields longer t .