Spain Mathematical Olympiad Problem 2
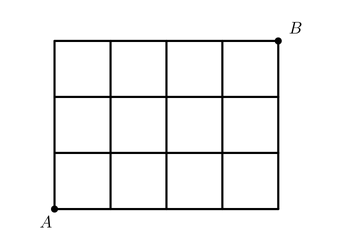 The figure shows a network of roads bounding
blocks. Person
goes from
to
and person
goes from
to
each going by a shortest path (along roads). The persons start simultaneously and go at the same constant speed. At each point with two possible directions to take, both have the same probability. The probability that the persons meet can be expressed as
where
and
are positive coprime integers. Find
.
This problem is part of
this set
.
The figure shows a network of roads bounding
blocks. Person
goes from
to
and person
goes from
to
each going by a shortest path (along roads). The persons start simultaneously and go at the same constant speed. At each point with two possible directions to take, both have the same probability. The probability that the persons meet can be expressed as
where
and
are positive coprime integers. Find
.
This problem is part of
this set
.
The answer is 293.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The problem is fairly straightforward. Note that a 'shortest' path is comprised of exactly 3+4=7 edges. Now, let's say that both A and B move at a speed of 1m/s and that each edge is of length 1 metre . Then, the possible positions of A at different times (in seconds) will be as shown: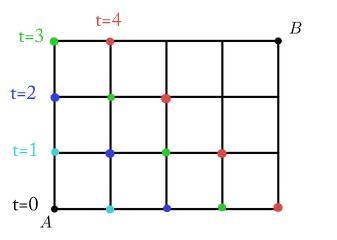
From this, and a similar consideration for B , it should be clear that they will meet at t=3.5 seconds at middle of the specific edges shown in the figure below: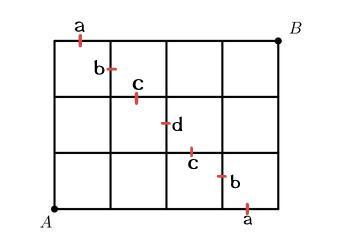
I have labelled certain edges with the same symbol because they are symmetric with respect to each other. That is to say that whatever probability corresponds to the upper edge a also corresponds to the lower edge a . This is basically equivalent to switching the positions of A and B . This will help us simplify the problem. Now, consider the case where A and B meet at the mid-point of edge d . For this, A must reach the point (2,1) (with A as origin) through any of the dotted red lines (the continuous red path for example), from the figure below: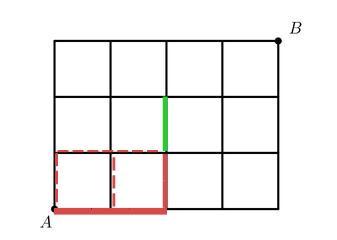
Thus, A has three possible paths to reach (2,1) Then, A must also choose the green path. At each junction, A has 2 choices, to go horizontal or to go vertical. Thus, the probability for this to occur is: P A , d = 3 ( 2 1 ) 3 ( 2 1 ) Using similar notation for B : P B , d = 3 ( 2 1 ) 3 ( 2 1 ) Thus, the probability of A and B to meet at d is: P d = P A , d . P B , d = 9 ( 2 1 ) 8 Note that the path that A and B choose after meeting does not affect this in any way. With similar reasoning, the other parts are easy: P c = 9 ( 2 1 ) 8 P b = 3 ( 2 1 ) 8 P a = ( 2 1 ) 7 Finally, the required probability is: P = 2 P a + 2 P b + 2 P c + P d Substituting the values, we get: P = 2 5 6 3 7 Which gives the answer: 3 7 + 2 5 6 = 2 9 3