Speak Louder!
You're making a megaphone by wrapping a piece of paper up as a simple cone and then cutting it at half of its height. The 2 new circular bases are parallel and left open at both ends for the air to flow through.
If this megaphone has a height of 24 cm. with a radius of 14 cm. at its bigger base, find its lateral surface area in .
If your answer is in a form of , then submit as your answer.
The answer is 525.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
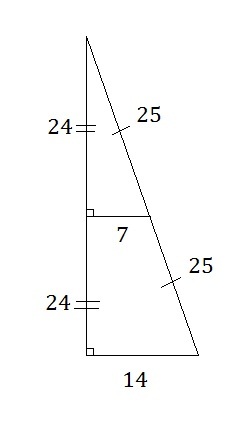
2 4 r = 4 8 1 4
r = 4 8 2 4 ( 1 4 ) = 7
The lateral area of a frustum of a right circular cone is given by
S = 2 1 ( c 1 + c 2 ) L
where: c 1 = circumference of the upper base, c 2 = circumference of the lower base and L = slant height
Substituting, we get
S = 2 1 π ( 1 4 + 2 8 ) 2 4 2 + 7 2 = 2 1 π ( 2 5 ) = 5 2 5 π
Finally,
A = 5 2 5