Special angle?
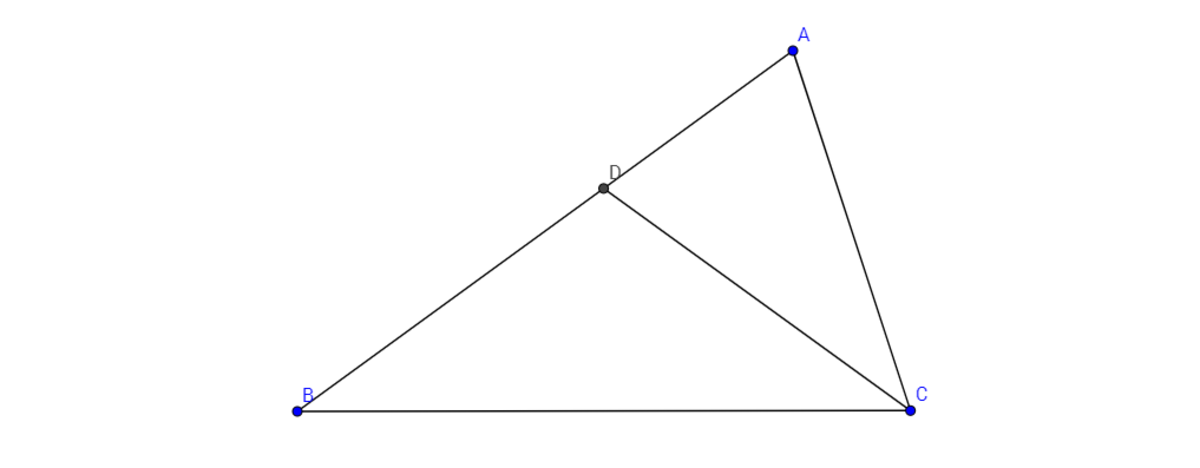
In a triangle , is double the size of Now, point is where the bisector of meets . Interestingly, . If radians, then
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Considering that angle A is double the size of angle B , we can bisect angle A like we did for angle C . Now suppose the angle bisector of angle A meets B C at point E such that angle A B C = angle B A E = angle C A E = x where x is the unknown angle. Considering that angle A B E =angle B A E , this tells us that A E = B E . Next join point D to E :
Considering that A C = B D as given in the question, A E = B E as determined and angle C A E = angle D B E , we see that triangles A C E and B D E are congruent employing S A S congruence. Now letting angle A C D = angle B C D = y , triangles A C E and B D E being congruent means C E = D E therefore angle C D E = angle D C E = y . Moreover, angle B D E = angle A C E = angle A C D + angle B C D = y + y = ( 1 + 1 ) y = 2 y .
With angle B A C being twice of angle A B C , angle B A C = 2 x therefore we have:
A C D + D A C = B D C
A C D + D A C = B D E + C D E
y + 2 x = 2 y + y
2 x = 2 y
x = y
Considering triangle A B C , we also have:
B A C + A B C + A C B = π
2 x + x + 2 y = π
( 2 + 1 ) x + 2 y = π
3 x + 2 y = π
Therefore with x = y ,
3 x + 2 x = π
( 3 + 2 ) x = π
5 x = π
x = 5 π
= > N = 5