Special Isosceles Trapezoid
The non-rectangular isosceles trapezoid with the smallest possible sum of its area and its perimeter, where all its angle bisectors meet at a single point and where both its area and its perimeter are integers, has a leg of q p , where p and q are relatively prime positive integers. Find p + q .
The answer is 9.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Label the isosceles trapezoid as follows:
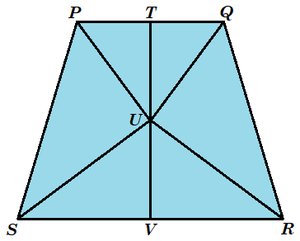
Let x = ∠ S P U = ∠ U P T = ∠ T Q U = ∠ U Q R and y = ∠ P S U = ∠ U S V = ∠ U R V = ∠ U R Q .
As a trapezoid, ∠ T P S + ∠ P S V = 1 8 0 ° , so 2 x + 2 y = 1 8 0 ° , which means x + y = 9 0 ° . Then by the angle sum of △ P U S , ∠ P U S = 1 8 0 ° − ( x + y ) = 1 8 0 ° − 9 0 ° = 9 0 ° . Similarly, ∠ Q U R = 9 0 ° .
Let a = P U = Q U , b = S U = R U , and c = P S = Q R . By the Pythagorean Theorem on △ P U S and △ Q U R , a 2 + b 2 = c 2 .
△ U V S ∼ △ P U S by AA similarity, so that S U S V = S P S U , or b S V = c b , which solves to S V = c b 2 and makes S R = c 2 b 2 . Also from the similarity, P U U V = S P S U , or a U V = c b , which solves to U V = c a b .
Also, △ P T U ∼ △ P U S by AA similarity, so that P U P T = P S P U , or a P T = c a , which solves to P T = c a 2 and makes P Q = c 2 a 2 . Also from the similarity, U S T U = S P S U , or b T U = c a , which solves to T U = c a b .
The perimeter of the trapezoid is then P = P Q + Q R + R S + S P = c 2 a 2 + c + c 2 b 2 + c , which after substituting a 2 + b 2 = c 2 simplifies to P = 4 c .
The area of the trapezoid is then A = 2 1 ( P Q + S R ) T V = 2 1 ( c 2 a 2 + c 2 b 2 ) c 2 a b , which after substituting a 2 + b 2 = c 2 simplifies to A = 2 a b .
From A = 2 a b , b = 2 a A , and from P = 4 c , c = 4 P , so that a 2 + b 2 = c 2 becomes a 2 + 4 a 2 A 2 = 1 6 P 2 , which solves to a 2 = 3 2 1 ( P 2 ± P 4 − 2 5 6 A 2 ) .
To have a real answer, the discriminant P 4 − 2 5 6 A 2 ≥ 0 , and to be a trapezoid (instead of a rectangle), a = b so the discriminant P 4 − 2 5 6 A 2 > 0 , which solves to P 2 > 1 6 A , whose smallest positive integer solutions are A = 1 and P = 5 .
Therefore, c = 4 P = 4 5 , so that p = 5 , q = 4 , and p + q = 9 .
Interestingly, the other lengths of the trapezoid also calculate to non-integer values of P Q = 2 0 1 ( 2 5 − 3 4 1 ) , R S = 2 0 1 ( 2 5 + 3 4 1 ) , T V = 5 4 , P U = Q U = 8 1 ( 4 1 − 3 ) , and S U = R U = 8 1 ( 4 1 + 3 ) .
Say the parallel sides of the trapezoid have lengths a and b and the non-parallel legs have length l ; let its area be A and perimeter P .
The angle bisectors of a quadrilateral meet in a single point if and only if the quadrilateral is tangential (see the link for a proof of this) - this means we can construct an incircle in the trapezoid.
As a tangential quadrilateral, we get two nice properties; firstly, a + b = 2 l = 2 P
so that P = 4 l ; secondly A = 2 r P
where r is the inradius of the trapezoid. For the trapezoid to exist, we need 2 r ≤ l . For it to satisfy a = b , we need 2 r < l .
Putting everything together, we have P = 4 l and A = 2 r l < l 2 = 1 6 P 2
Both of these are positive integers, so we need P 2 > 1 6 . The smallest possible perimeter is therefore P = 5 , and we can take A = 1 to minimise their total; finally l = 4 5 so the answer is 9 .
Just a sidenote - the condition A < 1 6 P 2 holds for any non-square quadrilateral, so we could get to that earlier.