Special Lines 2.

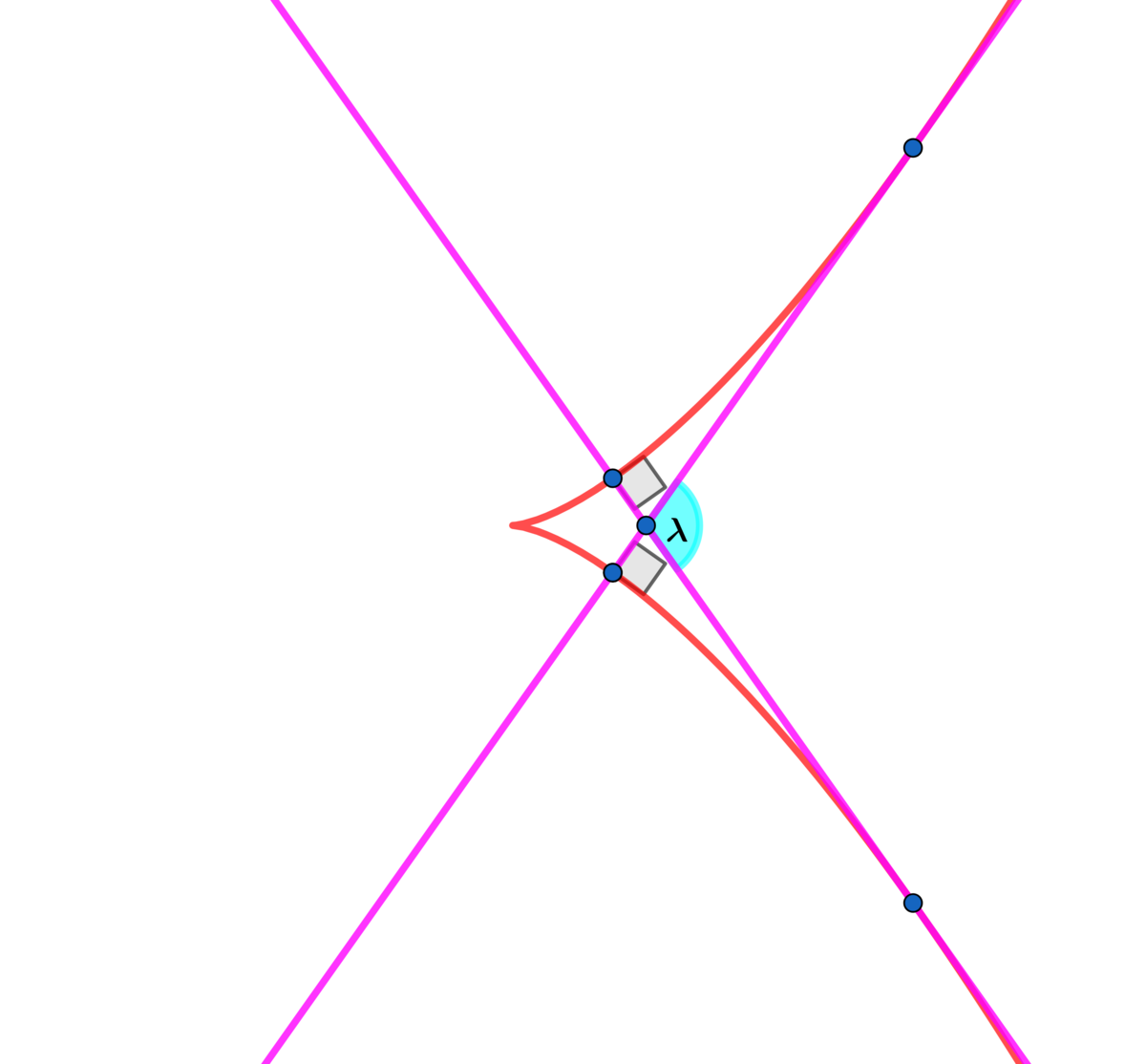
Let $x(t) = at^2 + b,\:\ y(t) = bt^3 + a \implies \dfrac{dy}{dx}|(t = t_{1}) = \dfrac{3b}{2a}t_{1} \implies$ the tangent line to the curve at $(x(t_{1}),y(t_{1}))$ is: $y - (bt_{1}^3 + a) = \dfrac{3b}{2a}t_{1}(x - (at_{1}^2+ b))$

Let the line be normal to the curve at $(x(t_{2}),y(t_{2})) \implies b(t_{2} - t_{1})(t_{2}^2 + t_{1}t_{2} + t_{1}^2) = \dfrac{3b}{2}t_{1}(t_{2} - t_{1})(t_{2} + t_{1}) \implies \dfrac{b}{2}(t_{2} - t_{1})(2t_{2}^2 - t_{1}t_{2} - t_{1}^2) = 0$ $t_{1} \neq t_{2} \implies t_{2} = -\dfrac{t_{1}}{2}$

Since the tangent is also normal to the curve at $(x(t_{2}),y(t_{2})) \implies \dfrac{9b^2}{4a^2}t_{1}t_{2} = -1$ $\implies \dfrac{9b^2}{8a^2}t_{1}^2 = 1 \implies t_{1} = \pm\dfrac{2\sqrt{2}a}{3b} \implies$ the two slopes are $\pm\sqrt{2}$ .

$\tan(\theta) = \sqrt{2} \implies \theta = \arctan(\sqrt{2}) \approx 54.73561 \implies \lambda = 2\theta \approx \boxed{109.47122}$ .

109.471 degrees is the dihedral angle of a regular octahedron

Interesting connection