Special Lines!
A line is "special" to a curve if it is both a tangent and a normal of the curve.
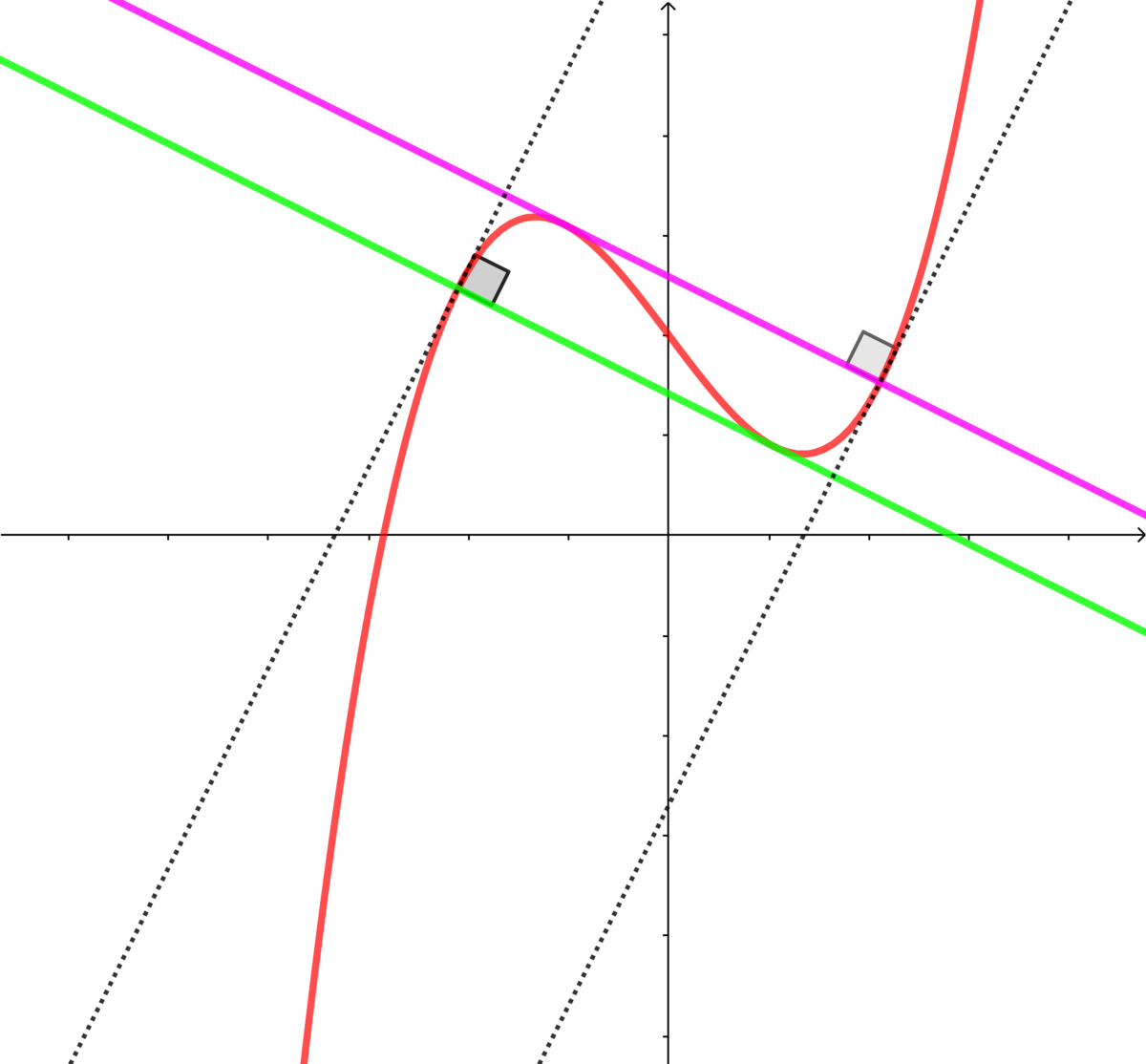
Only two lines are special to the curve x 3 + a x 2 + b x + c , where a , b , c are constants, and the two lines have the same slope.
What is this slope?
The answer is -0.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Brilliant solution!
m = 2 1 doesn't work because if it were true, then 4 m 2 − 4 m + 1 = 0 , implying that a 2 − 3 b = − 4 , which means f ′ ( t ) = 3 t 2 + 2 a t + 3 a 2 + 4 = 2 1 , which solves to t = 6 − 2 a ± 2 i , an imaginary number.
Log in to reply
I figured there had to be some a yielding real solutions and didn’t bother to check. Good find!
Log in to reply
Ivo! My reply to the obviously brilliant 15 year old XX from Taiwan. "Aha! Sorry X X, I didn't get that subtlety. Sometimes there are no lines and sometimes there are four lines but in one "super-special case, there are only two lines. What is the slope in that "super-special" case? Gotcha. Very clever. Armed with that new information I will look at the problem again. (Psst: It might be a good idea to say this in the question)"
Don't you mean m=-1/2 doesn't work as opposed to m=1/2 ?
where does (a^2-3b)^2=16 come from?
I don't know where you have gone wrong but -0.5 is not the answer. Take a simple example: y = x 3 − 3 x there are two solutions and four lines.
1a) Slope:-0.1188 x1=-0.980 x2=1.96.
1b) Slope:-0.1188 x1=0.980 x2=-1.96.
2a) Slope:-2.1317 x1=-0.538 x2=1.076.
2b) Slope:-2.1317 x1=0.538 x2=-1.076 .
Where x1 is the x value at the tangent and x2 is the x value at the intersection.
Log in to reply
Part of the problem is that you have to find the a , b , and c values of x 3 + a x 2 + b x + c so that there are only 2 "special" lines instead of 4 "special" lines.
Guys, the question is not phrased very well. The obviously brilliant 15 year old X. X. from Taiwan explained it to me. This was my reply "Aha! Sorry X X, I didn't get that subtlety. Sometimes there are no lines and sometimes there are four lines but in one "super-special case, there are only two lines. What is the slope in that "super-special" case? Gotcha. Very clever. Armed with that new information I will look at the problem again. (Psst: It might be a good idea to say this in the question)"
Let f ( x ) = x 3 + a x 2 + b x + c ⟹ f ′ ( x 0 ) = 3 x 0 2 + 2 a x 0 + b ⟹ the tangent line to the curve at ( x 0 , y 0 ) is y − ( x 0 3 + a x 0 2 + b x 0 + c ) = ( 3 x 0 2 + 2 a x 0 + b ) ( x − x 0 )
Let the tangent line be normal to the curve at ( x 1 , y 1 ) ⟹ ( x − x 0 ) ( x 1 2 + ( a + x 0 ) x 1 − ( 2 x 0 + a ) x 0 ) = 0
x 1 = x 0 ⟹ x 1 = − ( a + 2 x 0 )
Since the tangent is also normal to the curve at ( x 1 , y 1 ) ⟹ − 1 = ( 3 x 0 2 + 2 a x 0 + b ) ( 1 2 x 0 2 + 8 a x 0 + a 2 + b ) ⟹ 3 6 x 0 4 + 4 8 a x 0 3 + ( 1 9 a 2 + 1 5 b ) x 0 2 + 2 a ( a 2 + 5 b ) x 0 + ( a 2 + b ) b + 1 = 0 .
Let a = 0 ⟹ 3 6 x 0 4 + 1 5 b x 0 2 + b 2 + 1 = 0 ⟹ x 0 2 = 7 2 − 1 5 b ± 3 9 b 2 − 1 6 and letting 9 b 2 − 1 6 = 0 ⟹ b = ± 3 4 .
For real x 0 choose b = − 3 4 ⟹ x 0 2 = 1 8 5 ⟹ x 0 = ± 3 2 5 ⟹ m 1 = m 2 = − 2 1 .
how do you justify setting a=0?
Log in to reply
Refer to my above solution.
Setting a = 0 and finding a value of b , which in this case is b = − 3 4 , will give us equal slopes. I just choose the appropriate value of a and found a value of b so that the slopes are equal.
Using a = 0 and b = − 3 4 ⟹ 3 2 4 x 4 − 1 8 0 x 0 2 + 2 5 = 0 ⟹ x 0 2 = 1 8 5 ⟹ x 0 = ± 3 2 5 ⟹ m 1 = m 2 = − 2 1 .
I could have solved this problem in a simpler fashion as shown in some of the above posts.
The cubic can be translated on the plane without affecting the slope to transform it to f ( x ) = x 3 − a 2 x . With derivative f ′ ( x ) = 3 x 2 − a 2
( t , t 3 − a 2 t ) is some point on the curve and the tangent line has equation y − ( t 3 − a 2 t ) = ( 3 t 2 − a 2 ) ( x − t )
Solve f ( x ) = y to find where this line hits the cubic again: Besides x = t the equation x 3 − a 2 x = ( 3 t 2 − a 2 ) x − 2 t 3 has solution x = − 2 t
The slope of f ( x ) at this point is 1 2 t 2 − a 2
Now solve to find when the two slopes are perpendicular: ( 1 2 t 2 − a 2 ) ( 3 t 2 − a 2 ) = − 1 whose only real solutions are
a = ± 3 2 and t = ± 6 1 0
Finally, the slope is then 3 ( 6 1 0 ) 2 − ( 3 2 ) 2 = − 0 . 5
In retrospect using a instead of a 2 in the original cubic would have been simpler, but I originally thought in terms of the x-intercepts being ( ± a , 0 ) .
Your first equation should be f ( x ) = x 3 − a 2 x ?
Note that you should ideally use f ( x ) = x 3 − a x , in part because your current formulation doesn't allow you to deal with x 3 + x unless you allow for purely imaginary a .
Log in to reply
Thanks for the correction.
I pointed out at the bottom that a 2 was not the ideal choice. I had already typed everything up and didn't feel like changing it since the solution still works. x 3 + x is easily ruled out since it's obvious that no normal will touch the curve again.
This problem reminds me of an earlier problem on Sept-03, where the square of maximum area was placed on cubic curve.
Here too, assuming symmetry around the origin, the cubic curve is y=x^3-gx, where g is to be found within the given constraints of the tangent cutting the curve as a normal.
In the Sept-03 problem, g=√8, while here, it is g= 4/3, and after some algebra,
the slope of tangent/normal = -(1/2).
f ( x ) = x 3 + a x 2 + b x + c
f ′ ( x ) = 3 x 2 + 2 a x + b
For convenience, let the point of tangency of a special line have coordinates ( t , f ( t ) ) and the point of intersection, where the special line is normal to the curve, have coordinates ( n , f ( n ) ) .
We have:
f ′ ( t ) ⋅ f ′ ( n ) = − 1
t − n f ( t ) − f ( n ) = f ′ ( t )
Second equation leads to ( n − t ) ( n + a + 2 t ) = 0 ⟹ n = − a − 2 t .
Substituting into the first and using m = f ′ ( x ) , this yields ( 3 t 2 + 2 a t + b ) ⋅ ( 1 2 t 2 + 8 a t + a 2 + b ) = − 1 ⟹ 4 m 2 + ( a 2 − 3 b ) m + 1 = 0 . Since the slopes of the two lines is the same, this quadratic equation must only have one root, implying ( a 2 − 3 b ) 2 = 1 6 ⟹ 4 m 2 ± 4 m + 1 = 0 ⟹ m = ∓ 2 1 . However, m = 2 1 leads to a non-real t .