Special Medians of a Triangle
In triangle A B C , D is the midpoint of A C and E is the midpoint of A B . B D and C E are perpendicular to each other and intersect at the point G . If A B = 7 and A C = 9 , what is the value of B C 2 ?
The answer is 26.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
11 solutions
We know that \overline{BD} and \overline{EC} are medians because they connect the midpoint of a side of the triangle and the opposite vertex. Therefore the centroid (point G) separates \overline{EC} into ratios of 1:2 and \overline{BD} into ratios of 1:2. Set \overline{BG} as 2x, \overline{GD} as x, \overline{CG} as 2y and \overline{GE} as y. By Pythagorean Theorem, x^2 + 4y^2 = (\frac{9}{2})^2 and 4x^2 + y^2 = (\frac{7}{2})^2. We desire 4x^2 + 4y^2 because this will equal (\overline{BC})^2. Adding both equations together leads to 5x^2+5y^2 = \frac{65}{2}. 4x^2+4y^2 = 26.
Let BD be 3x and CE be 3y
So by the property of Centroid,
G
D
B
G
=
G
D
C
G
=
1
2
Also,
B
E
2
=
E
Y
2
+
B
Y
2
2
7
2
=
y
2
+
(
2
x
)
2
4
4
9
=
y
2
+
4
x
2
Eq. No.: 01
Similarly,
C
D
2
=
G
D
2
+
C
G
2
2
9
2
=
x
2
+
(
2
y
)
2
4
8
1
=
x
2
+
4
y
2
Eq. No.: 02
Upon adding Eq. 1 and Eq. 2 we get,
5
×
(
x
2
+
y
2
)
=
4
1
3
0
Upon multiplying this by
5
4
we get,
4
x
2
+
4
y
2
= 26
(
2
x
)
2
+
(
2
y
)
2
= 26
B
G
2
+
G
C
2
= 26
B
C
2
= 26
Because angles BGE and CGD are right angles, it can be concluded via the Pythagorean Theorem that E G 2 + B G 2 = 3 . 5 2 , and C G 2 + D G 2 = 4 . 5 2 . Furthermore, D G 2 + E G 2 = D E 2 . Because DE is the midline of triangle ABC (D and E are respective midpoints of the sides they are on), its length must be half that of BC. Finally, B G 2 + C G 2 = B C 2 . Substituting and simplifying: B C 2 = B G 2 + C G 2 , B C 2 = 3 . 5 2 - E G 2 + 4 . 5 2 - D G 2 , B C 2 = 32.5 - ( E G 2 + D G 2 ), B C 2 = 32.5 - E D 2 , B C 2 = 32.5 - ( B C / 2 ) 2 , ( 5 / 4 ) B C 2 = 32.5, B C 2 = 26
Let CG=a, GE=b, GB=c, GD =d, and BC=x. Using Pythagoras, we have a^2 + c^2 = x^2 ...(1), a^2 + d^2 = 4.5^2 .....(2), and b^2 + c^2 = 3.5^2 ........(3). We add (2) and (3) these 3 to get a^2+b^2+c^2+d^2 = 4.5^2+3.5^2. Substitute (1) to this equation. then we have x^2 + b^2+d^2 = 4.5^ + 3.5^. But b^2+d^2 is (DE)^2 which is (0.5 x)^2. So we have 0.25x^2 + x^2 = 32.5, then we find x^2 = (BC)^2 = 26
Noting that the triangles EBG, CGD, GCB and DEG are right triangles we deduce the validity of the following reports:
EB^2-BG^2=GE^2
DC^2-CG^2=GD^2
CG^2+GB^2=CB^2
DG^2+GE^2=DE^2
So:
EB^2-BG^2+DC^2-CG^2=GE^2+GD^2=DE^2
So:
EB^2+DC^2-(BG^2+CG^2)=DE^2,
EB^2+DC^2-CB^2=DE^2.
Observing that:
CB^2=4DE^2 (CB=2DE)
we may write:
EB^2+DC^2-CB^2=(CB^2)/4.
SO:
EB=7/2, CD=9/2
CB^2=26
Medians are divided in 2:1 by centroid, thus
GE=b and GC=2b for some a and b GD=a and GB=2a
By Pythagoras Theorem,
(2a^2) + (b^2) = ((7/2)^2), (2b^2) + (a^2) = ((9/2)^2)
Solving the two for positive a and b, we get
a=(sqrt(23/3))/2 and b=(sqrt(55/3))/2
Again by Pythagoras,
(BC)^2 = (2a)^2 + (2b)^2 = 78/3 = 26
Since B D and C E are medians, thus A E = E B , A D = D C and D E is parallel to B C . It also follows that triangles A D E and A C B are similar, thus D E B C = A E A B = 2 ⇒ B C = 2 D E . Since D E is parallel to B C thus ∠ E D B = ∠ D B C and ∠ D E C = ∠ E C B , which implies that triangles D E G and B C G are similar by angle-angle-angle and a factor of D E B C = 2 .
Let G D = x and G E = y , so we have B G = 2 x and C G = 2 y . Applying the Pythagorean theorem on triangles G E B , G D C and G B C , we have 4 A B 2 = E B 2 = 4 x 2 + y 2 , 4 A C 2 = D C 2 = x 2 + 4 y 2 and B C 2 = 4 x 2 + 4 y 2 . Adding the first two equations, we have
4 A B 2 + A C 2 B C 2 = 5 x 2 + 5 y 2 = 4 5 B C 2 = 5 A B 2 + A C 2 = 5 7 2 + 9 2 = 2 6
In triangle A B C , D is the midpoint of A C and E is the midpoint of A B . B D and C E are perpendicular to each other and intersect at the point G .
Because G is median and B D and C E are perpendicular to each other, implies C G = 2 E G and B G = 2 D G and we got 3 right triangle of C G D , B G E and B G C .
Just do with Pythagorean theorem on each triangle.
Let see in triangle C G D
C G 2 + D G 2 = C D 2
because C D = 2 C A = 2 9 and D G = 2 B G
C G 2 + ( 2 B G ) 2 = ( 2 9 ) 2
4 C G 2 + B G 2 = 9 2 .. (1)
in triangle B G E
B G 2 + E G 2 = B E 2
because B E = 2 B A = 2 7 and E G = 2 C G
B G 2 + ( 2 C G ) 2 = ( 2 7 ) 2
4 B G 2 + C G 2 = 7 2 ... (2)
and in triangle B G C
B C 2 = C G 2 + B G 2 ... (3)
Let's sum (1) and (2) we'll got
5 B G 2 + 5 C G 2 = 9 2 + 7 2 divide it with 5
B G 2 + C G 2 = 5 9 2 + 7 2
and subtitute to (3)
B C 2 = 5 9 2 + 7 2 = 2 6
BD is a median of the triangle, so BG = 2 DG. Similarly, CG = 2 EG. Let DG = a and EG = b. Then, by Pythagorean theorem on triangle BGE, 4a^2+b^2=(7/2)^2=49/4. By Pythagorean theorem on triangle CGD, a^2+4b^2=(9/2)^2=81/4. Adding gives 5a^2+5b^2=130/4=65/2, so a^2+b^2=13/2.
What we want to find is BC^2 which is 4a^2+4b^2 by Pythagorean theorem again. This is 4*13/2=26.
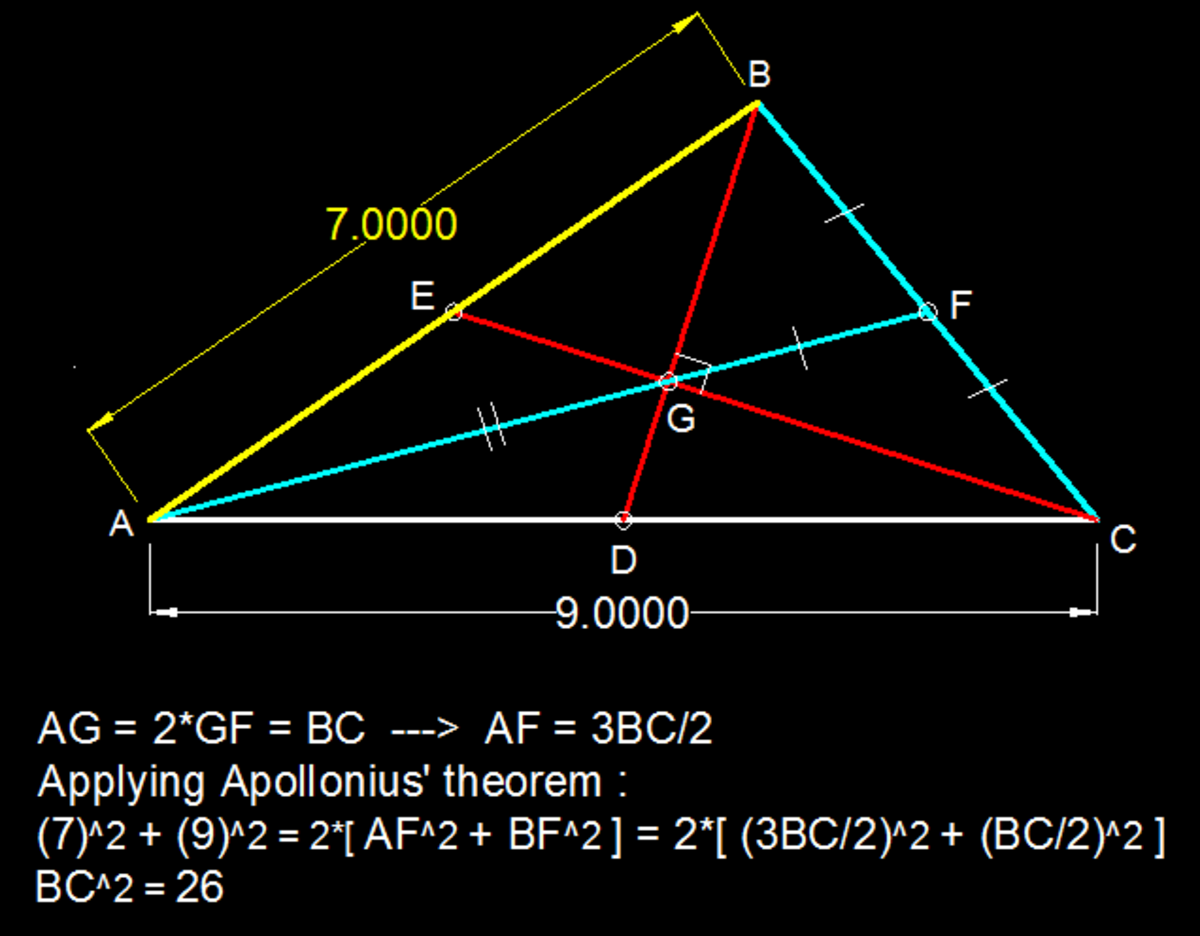
Draw an extra line between D E
Triangle A D E is similar to Triangle A B C
If we say B C is x , means D E is 2 x
We can say :
x 2 = B G 2 + C G 2
( 2 x ) 2 = D G 2 + E G 2
Adding them up would be :
4 5 x 2 = ( B G 2 + E G 2 ) + ( C G 2 + D G 2 )
4 5 x 2 = ( 2 7 ) 2 + ( 2 9 ) 2
4 5 x 2 = 4 4 9 + 4 8 1
5 x 2 = 4 9 + 8 1
x 2 = 5 1 3 0 = 2 6