Special Rectangle
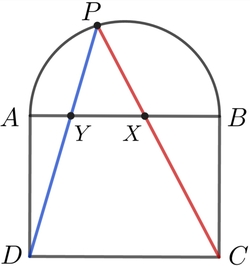
A semicircle is drawn on the side A B of a rectangle A B C D .
Let P be a point on the semicircle, and let X and Y be defined as shown in the diagram.
If the value A X 2 + B Y 2 is independent of the position of P , then find A B A D .
The answer is 0.7071067812.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Let ∣ A B ∣ = a , ∣ A D ∣ = b . Consider two positions of the point P , one at A and the other at the midpoint of the semicircular arc. In the first case, points A , P , X , Y are identical, so that ∣ A X ∣ 2 + ∣ B Y ∣ 2 = a 2 . In the second case, ∣ A X ∣ = ∣ B Y ∣ = a + 2 b a 2 + a b ⟹ ∣ A X ∣ 2 + ∣ B Y ∣ 2 = 2 a 2 ( a + 2 b a + b ) 2 . So a 2 = 2 a 2 ( a + 2 b a + b ) 2 ⟹ a 2 = 2 b 2 ⟹ a b = 2 1 ≈ 0 . 7 0 7 1 0 6 7 8 1 2 .
Exactly what I did. Peace to you bro
I used the two easiest positions where P is at B and P is at the midpoint of the arc. From there I used similar triangles and worked out AC in terms of AY, and using that special case I found the ratio.
 It is true for circle.
It is true for circle.
The problem looks slightly daunting at first, but when really thinking about it, one can find out the constant value of A X 2 + B Y 2 using a simple case.
This simple case is such:
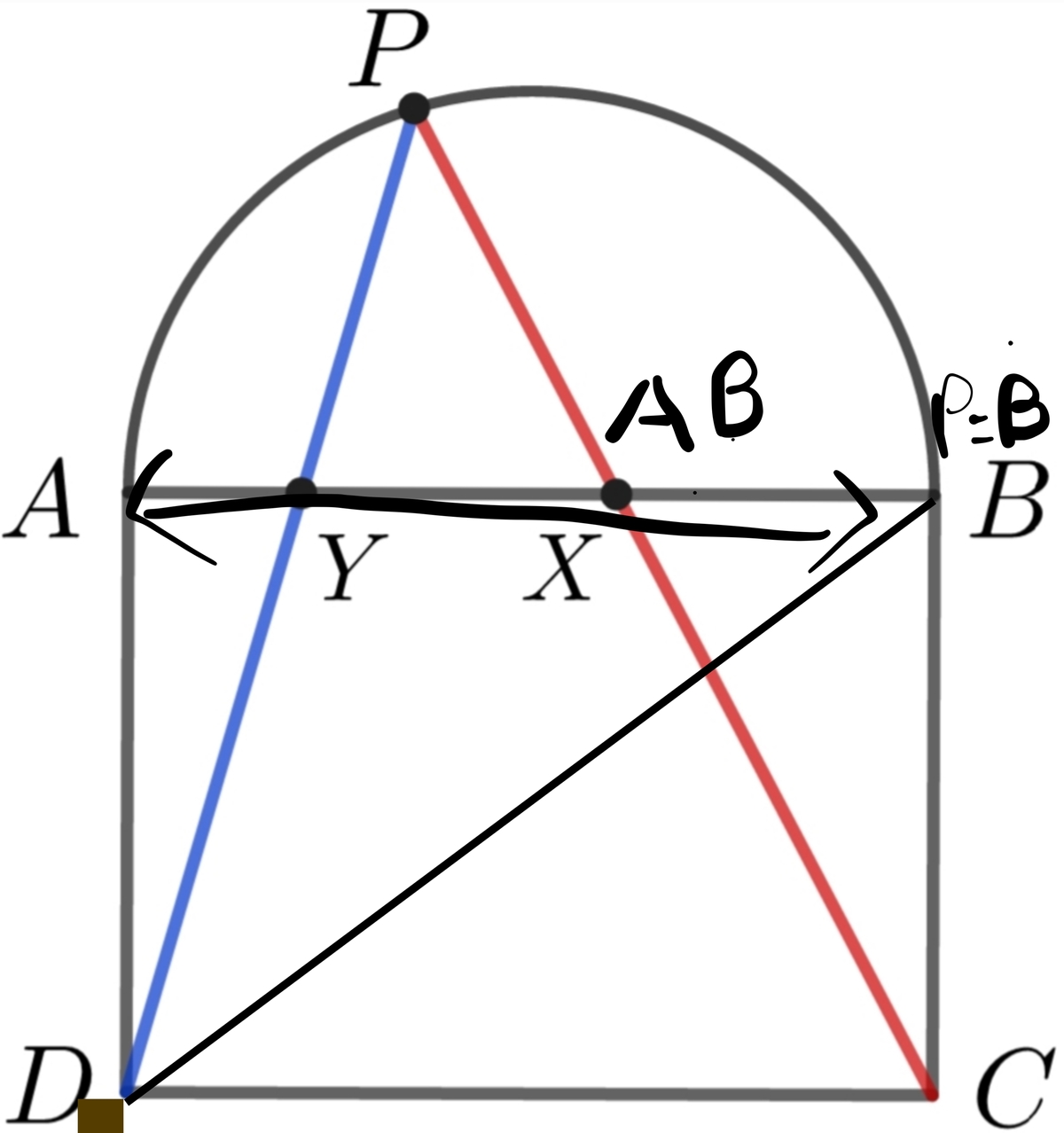
When P is at point B, or A, assuming that the value of A X 2 + B Y 2 is constant for all points of P, the value of A X 2 + B Y 2 = A B 2 + 0 + 0 = A B 2
We have just deduced that the value of A X 2 + B Y 2 which will remain constant will be A B 2 .
Using algebra, we can apply this to the example of P being at the top of the semicircle. If P is at the top, then we can visualise the divisions created by the triangle of A B like this:
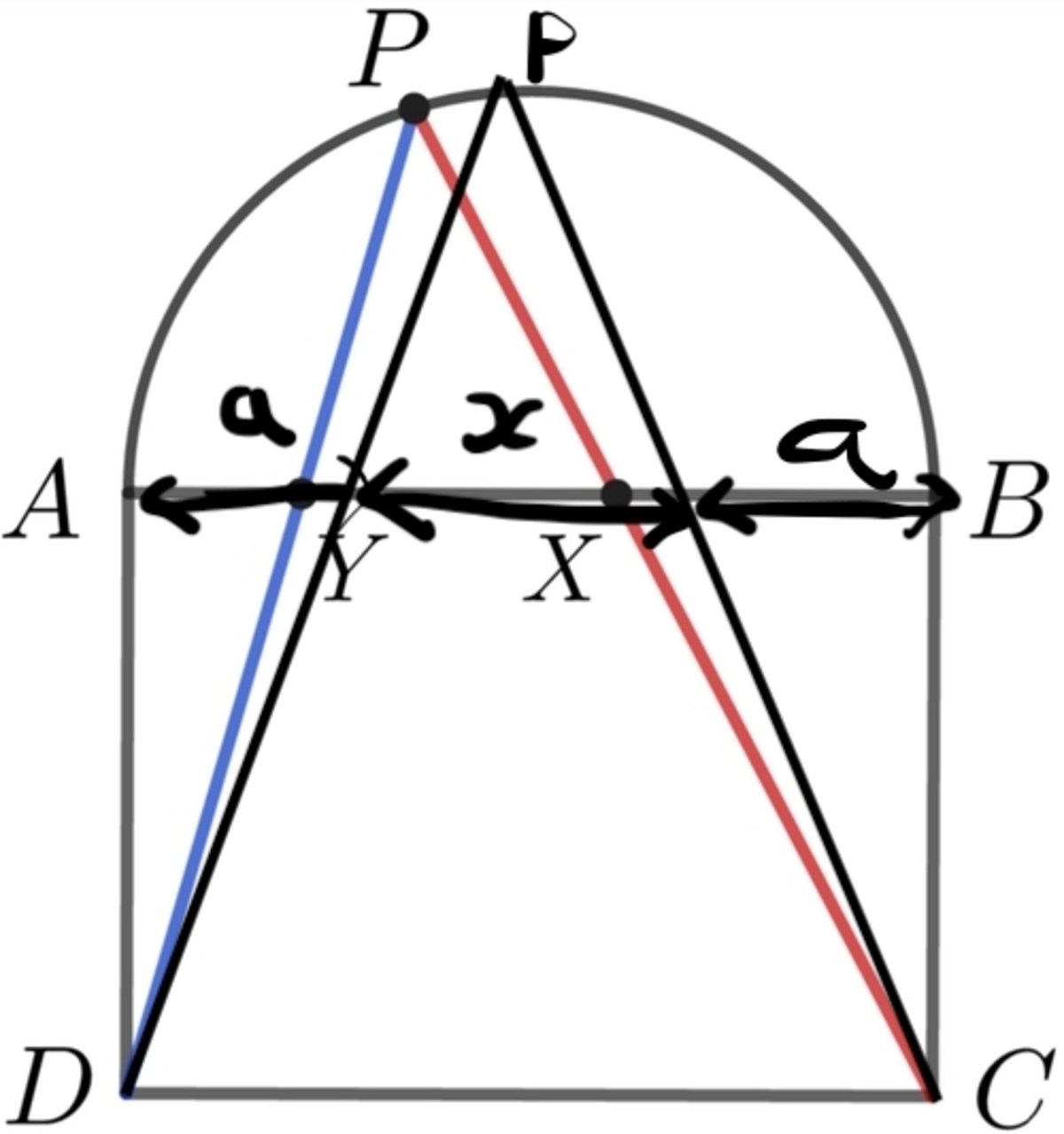
The triangle's points Y and X divide A B 's segments A Y and B X equally, and this can be written algebraically as a . Hence the total length of A B is 2 a + x
Therefore, combining the fact that the constant value of A X 2 + B Y 2 = A B 2 and the constant value for this case where P is at the top is 2 ( a + x ) 2 , we can write the equation as follows:
2 ( a + x ) 2 = ( 2 a + x ) 2
This simplifies into 2 a 2 + 4 a x + 2 x 2 = 4 a 2 + 4 a x + x 2
Simplifying, we get: 2 a 2 = x 2
Therefore x = 2 a
Therefore, using similar triangles for case 2 where P is at the top of the semicircle, we can find AD in terms of a by equating the ratios of height and base:
x 2 1 A B = A B 2 1 A B + A D
Which is:
2 a 2 1 ( 2 a + 2 a ) = 2 a + 2 a 2 1 ( 2 a + 2 a ) + A D
Isolating AD, we get A D = ( 1 + 2 ) a
writing the ratio and cancelling the a s, we get 2 + 2 1 + 2
Which is equal to 0 . 7 0 7 1 0 6 7 8 1 2
I used the two particular cases : X=A and X=centre of circle. And then I used Thalès twice.
We consider two position of P.First one is when P coincides with A.That gives us, A X 2 + B Y 2 = A B 2 .Then we consider when P is the midpoint of the arc AB.In that case we get two equations, ( 1 − 2 1 ) ∗ c o t θ = k and c o t θ = 2 k + 1 where k = a b A D and θ = a n g l e A D Y . Solving these two eqautions gives us the value of k.
Let the semicircle be of radius 1 and its center be the origin of the x y -plane, B C = A D = h and P ( x , y ) . Let A X = a and B Y = b . Then
⎩ ⎪ ⎨ ⎪ ⎧ a = 1 + x + y + h y ( 1 − x ) = 1 + y + h y + h x b = 1 − x + y + h y ( 1 + x ) = 1 + y + h y − h x
⟹ When ⎩ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎧ x = − 1 , x = 0 , x = 1 , y = 0 y = 1 y = 0 ⟹ a = 0 , b = 2 , ⟹ a = b = h + 1 h + 2 , ⟹ a = 2 , b = 0 , a 2 + b 2 = 4 a 2 + b 2 = 2 ( h + 1 h + 2 ) 2 a 2 + b 2 = 4
For a 2 + b 2 to be independent of ( x , y ) , then 2 ( h + 1 h + 2 ) 2 = 4 ⟹ h = 2 . Putting it in a and b .
⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ a = y + 2 2 y + 2 x + 2 b = y + 2 2 y − 2 x + 2
Then
a 2 + b 2 = ( y + 2 2 y + 2 x + 2 ) 2 + ( y + 2 2 y − 2 x + 2 ) 2 = ( y + 2 ) 2 2 ( 2 y + 2 ) 2 + 4 x 2 = ( y + 2 ) 2 8 y 2 + 8 2 y + 4 + 4 x 2 = y 2 + 2 2 y + 2 4 y 2 + 8 2 y + 8 = 4 Note that x 2 + y 2 = 1
That is a 2 + b 2 is independent of ( x , y ) when h = 2 and A B A D = 2 h = 2 2 ≈ 0 . 7 0 7 .