Speed Calc sans Radar

Algebra Level pending

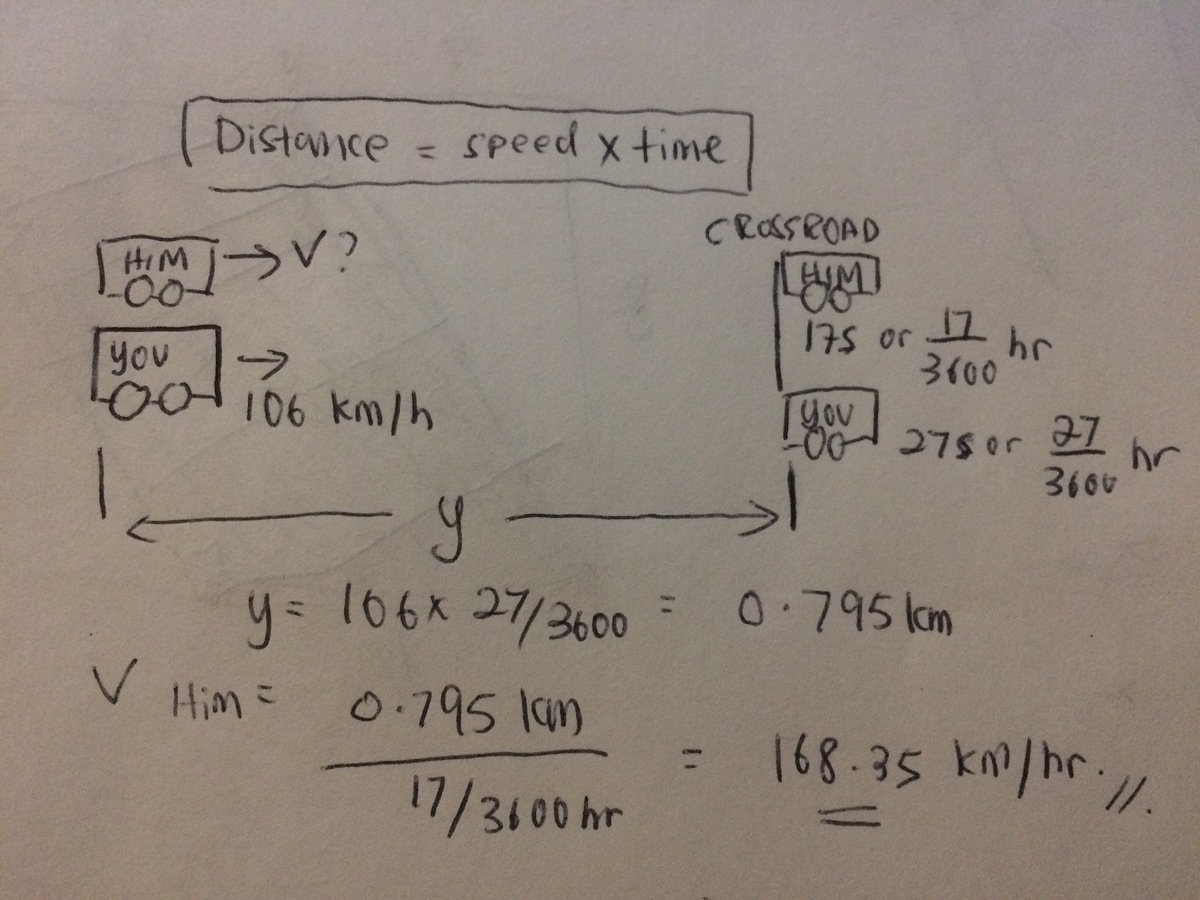
I was driving to our neighboring city yesterday when I noticed a car overtaking us at a high speed. As soon as the car passed us I started to count out seconds until the car reached a crossroad and continued to count until we reached the same crossroad. If the first count was 17 and the second count was 27 and I maintained a uniform speed of 106 km/hr how fast was the other car going? Assume it also maintained a uniform speed. Give the answer to the nearest km/hr.


The answer is 168.

Guiseppi Butel by Guiseppi Butel , 90, Canada

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

3 solutions

1 Helpful 0 Interesting 0 Brilliant 0 Confused
Genis Dude
Feb 6, 2017

Let the both travel 'x' distance.

Speed of our car is 106km/h =((53*5)/9) m/s

Speed =x/time

Therefore,(53*5)/9=x/27

→x=3*265

Speed of their car = x/time

→3*265/17

~168.3

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Guiseppi Butel
Feb 5, 2017

D= r*t

D1 = r1 * t1,

D2 = r2 * t2, but D1 = D2, therefore

r1 * t1 = r2 * t2

or r2 = (r1* t1)/t2

(27*106)/17 = 168

0 Helpful 0 Interesting 0 Brilliant 0 Confused

Can you write a solution that is helpful to those who cannot solve it? Else I'm inclined to delete this solution to encourage others to contribute a relevant answer.

Brilliant Mathematics Staff - 4 years, 4 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...