Sphere in Swimming Pool
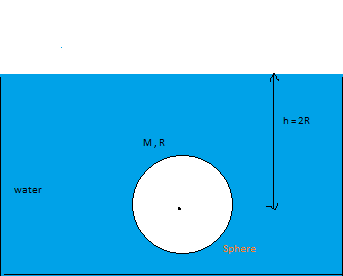
Find The net upward Force exerted by the liquid of an Swimming Pool on the uniform sphere on bottom half sphere . Neglect atmospheric pressure . If Radius of sphere is 'R' and it is at the depth 'h' from the upper upper surface of swimming pool. And density of liquid is ρ It can be Express as : F u p w a r d = b a π ρ g R c
Find a + b + c
This is part of My Set Deepanshu's Mechanics Blast
The answer is 14.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
ohh Nice ( in fact awesome :) ) , I was Trying To do it with integration , and as always This time also Deepanshu Set really well question !
But Isn't You Forget to writing Density everywhere in Solution ?
Log in to reply
Can you post the integration method. I also tried to use that but got a very little bit difference in answer. I took the projection of every infinitesimal disc of radius x on horizontal plane (Perpendicular to direction of applied Upward Buoyant force).
Please post your approach too.
Log in to reply
Yeah!I did this by integration and It is not so hard.
oh yeah, I did sorry,should have double checked
Very nice question and very very nice solution.
I didn't notice this shortcut... Nice solution.
Can you explain it in detail, not able to understand fully
Log in to reply
Since the fluid is at rest , so all its components must be in equillibirum, moreover, the force exerted does not depend on the properties of the object dispersed in it other than volume, so instead of the sphere, just imagine a cylindrical column of water with a spherical end (test tube), and then consider its equillibrium.
amazing from where did you get the inspiration of solution.
let me tell a good method ..... F u p w a r d - F D o w n = buoyant force , since buoyant force can be easily calculate from it's volume, thew answer you get will provide a = 8 , b= 3 , c= 3 , easy enough ! :)
Archimedes' Principle can be used. In this scenario, there are 2 forces: upward and downward force, both exerted by the fluid. However, upward > downward, so there's a buoyant force (Fup - Fdown = Fbuoy = weight of water displaced). The forces vary throughout the sphere's surface, so here's the trick: split the sphere in half such that we only consider the bottom half of the sphere (force exerted on bottom of sphere won't change in both cases). Since the top of the bottom hemisphere is a circle, we know Fdown right away, and can use it to find Fup.
well i did it with integration!.(and got d right answer!) step 1: take a small ring element which subtends an angle (theta) at the centre next write the expressesion for force at that small area and multiply it by cos(theta) because by symmetry the sine theta components cancels out you will get something like this 2πR^2 ρg[h sin(theta)*cos(theta) + Rsin(theta) * cos^2(theta)]• d(theta) (dA = 2πR^2 *sin(theta)•d(theta) NOW INTEGRATE,PUTTING LIMITS FROM(0,π/2)
Forget the sphere. Instead just imagine a water column that extends from the surface to the depth of the sphere such that its upper end is a cylinder of radius R, and the lower end has a spherical end (like the lower end of a test tube) with radius R,
BASICALLY A HEMISPHERE ATTACHED TO CYLINDER OF HEIGHT 2R and RADIUS R
Clearly this is in equilibrium , because this is a water column in a water body, so its weight is equal to the upper force exerted by lower part of water, or
F = W = m g = 3 2 ρ π R 3 g + ρ π R 2 g ( 2 R ) = 3 8 ρ π R 3 g .
or answer is 14 !
Nice innovative problem !