Sphere Surface Dynamics - Bird's Nest
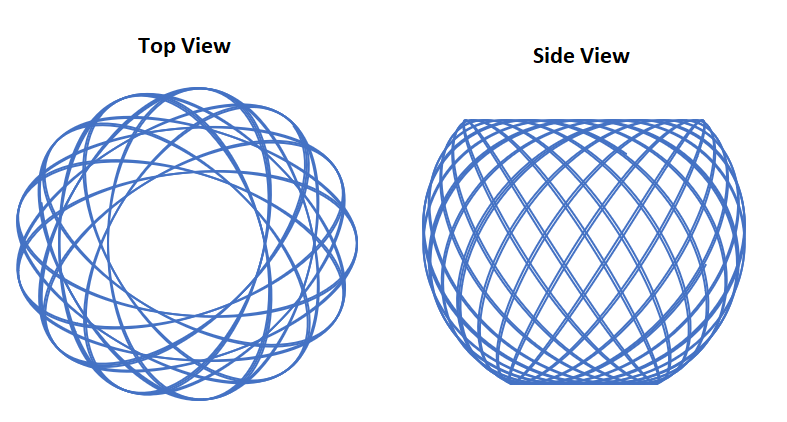
A massive particle is confined to the surface of a unit-sphere centered on the origin in the coordinate system. The particle moves without energy losses over the surface of the sphere.
At time (seconds), the particle's position and velocity are described as follows (SI units):
There is an ambient gravitational acceleration of in the (downward) direction. The system dynamics cause the particle to trace out a "bird's nest" pattern on the surface of the unit-sphere.
What is the particle's -coordinate (in meters) at time (seconds)?
Note: This exercise requires numerical integration
The answer is 0.6066.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
This sort of problem lends itself perfectly to a Lagrangian Mechanics solution. Define the spatial coordinates (I'm going to drop the parentheses for the trig arguments):
x = c o s θ c o s ϕ y = s i n θ c o s ϕ z = s i n ϕ
Derive the x y z velocities:
x ˙ = c o s θ ( − s i n ϕ ϕ ˙ ) + c o s ϕ ( − s i n θ θ ˙ ) y ˙ = s i n θ ( − s i n ϕ ϕ ˙ ) + c o s ϕ ( c o s θ θ ˙ ) z ˙ = c o s ϕ ϕ ˙
Particle kinetic energy:
E = 2 1 m v 2 = 2 1 m ( x ˙ 2 + y ˙ 2 + z ˙ 2 ) = 2 1 m ( ϕ ˙ 2 + c o s 2 ϕ θ ˙ 2 )
Particle potential energy:
U = m g z = m g s i n ϕ
Lagrangian:
L = E − U = 2 1 m ( ϕ ˙ 2 + c o s 2 ϕ θ ˙ 2 ) − m g s i n ϕ
Equations of Motion:
d t d ∂ θ ˙ ∂ L = ∂ θ ∂ L d t d ∂ ϕ ˙ ∂ L = ∂ ϕ ∂ L
Results of evaluating equations of motion:
ϕ ¨ = − s i n ϕ c o s ϕ θ ˙ 2 − g c o s ϕ θ ¨ = 2 t a n ϕ θ ˙ ϕ ˙
Numerically integrating for 30 seconds and plotting yields the beautiful "bird's nest" pattern seen in the problem statement. At t = 3 0 , x ≈ 0 . 6 0 6 6 .