Spheres n' Probability

Geometry Level 1

4 points are randomly chosen on a sphere to form a tetrahedron.

What is the probability the center of the sphere will be in the tetrahedron?

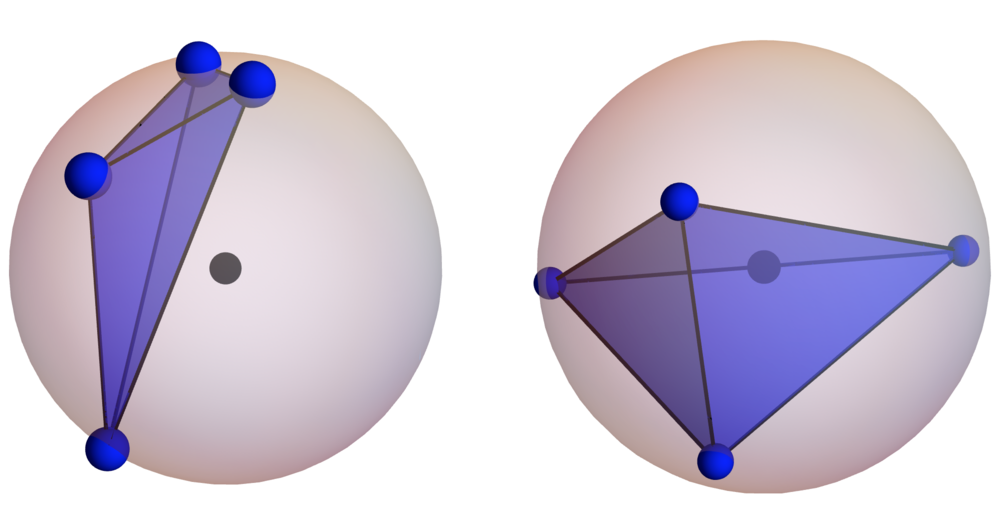On the left, the center of the sphere <strong>isn't</strong> inside the random tetrahedron. On the right, it <strong>is</strong>. On the left, the center of the sphere isn't inside the random tetrahedron. On the right, it is .

1 8 \frac18 1 4 \frac14 3 8 \frac38 1 2 \frac12

David Marji by David Marji , 16, Saudi Arabia

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

7 solutions

John Ross
Apr 1, 2018

I could try to write a solution, but this video explains it much better than I ever could.

72 Helpful 0 Interesting 0 Brilliant 0 Confused

Yeah, this is a famous Putnam Problem.

BLCRAFT Gaming - 3 years, 2 months ago

I love this problem.

Rajas Ketkar - 3 years, 2 months ago

Classic 3b1b

Ankit Agarwal Staff - 3 years, 2 months ago

For Chinese users who cannot log into YouTube, watch this: https://www.bilibili.com/video/av17275211

Yifei Xu - 3 years, 2 months ago
Idan Zur
Apr 2, 2018

3B1B did a great video on this topic

29 Helpful 0 Interesting 0 Brilliant 0 Confused
Andre Bourque
Apr 1, 2018

A friend and I solved this and its higher dimensional analogs as a research problem. Unbeknownst to us it appeared on the Putnam! However, our solution was much different than the one that is mentioned in the video that popularized this question. (I will point out that it is possible to set up a triple integral that can equate this probability) Essentially we unwrapped the surface of the sphere into a square with wrap around properties (this has a topological name). We made the observation that on average the four points took up a fourth of this square; however, this region included the "good and bad" regions so we divided by two. There is much rigor and detail to the solution that I left out but that is the jist.

14 Helpful 0 Interesting 0 Brilliant 0 Confused

It is one of the best problems in Putnam competition. When I saw it for the first time I thought of bijectionbetween sphere minus the noth pole and the plane. This we do in complex analysis. It is called stero graphic projection. Then instead of choosing points on sphere we can choose points on plane. We can write down whether condition when the origin is inside the tetrahedron in terms of the points on the plane. It is a horrible way of solving problems. I was shocked when I saw the solution. It is too simple.

Srikanth Tupurani - 3 years, 2 months ago

If we take the problem of circle. The problem is three points are randomly chosen on the circle.2what is the probability that the triangle formed by the three points contains origin. This can be solved by solving a discre problem consider n points on the circle equally spaced. We are randomly selecting three points what is the probability that origin lies in the triangle formed by these three points. What ever answer we get say f(n) as n tends to infinity it will tend to the answer of the original problem. We cannot repeat the same idea in case of sphere it becomes messy.

Srikanth Tupurani - 3 years, 2 months ago

I guess that in n dimensions the answer would be 2^(- n), right?

Pau Cantos - 3 years, 2 months ago

Hello all, I solved this using MS Excel simulation. Check this out:

https://m.youtube.com/watch?v=tqrYAfNeUbk

Si T - 3 years ago
Joseph Johannes
Apr 2, 2018

For any 4 points you choose, you can draw 4 lines through 1 point and the centre of the sphere.

Then, you get 4 more points at the intersection of the 4 lines and the sphere. This means you have 4 pairs of points that are diametrically opposite.

If you connect any three of the 4 original points (which you can select in 4 possible ways), one of the points in the remaining pair will yield a tetrahaedron enclosing the centre, and the other a tetrahaedron without the centre.

This means that we have 4 possible ways to choose the original 3 points and 2 ways to choose the 4th point, out of which only 1 possible selection will yield the desired tetrahaedron: p = 1 4 ⋅ 2 = 1 8 p = \frac{1}{4\cdot 2} = \frac{1}{8}

5 Helpful 0 Interesting 0 Brilliant 0 Confused

What if you choose two pairs of diametrically opposite points?

Ajay Kumar - 3 years, 2 months ago

Log in to reply

As there are an infinite number of points to choose from, the chance of choosing two which are diametrically opposite is effectively 0 so this doesn't change the results. However, it's always a good idea to consider these sorts of situations and there's a whole branch of mathematics called measure theory which was developed to take account of such things.

Richard Farrer - 3 years, 2 months ago
A I
Apr 6, 2018

In order for the tetrahedron not to enclose the center, all four points have to be on one side of the sphere. The position of the first point doesn't matter as it can be chosen randomly; and each of the remaining points have a half chance of being in the "right half of the sphere". Therefore for them all to be in the same side there is a chance of (1/2)^3 which is 1/8.

3 Helpful 0 Interesting 0 Brilliant 0 Confused

How can the second point ever be in the "wrong half of the sphere"? It will always lie on a great circle with the first point

Richard Farrer - 3 years, 2 months ago

You have to specify a distinct hemisphere to determine if points are on that hemisphere, or not. Fixing the first point does not specify a distinct hemisphere. It could be on infinite many hemispheres.

Using hemispheres you could go like this:

Three random points will always be on some common hemisphere. Take three of the four random points, P1, P2, and P3. Divide the sphere by the plane defined by the sphere center, P1, and P2. Now P4 must be on the hemisphere not containing P3. Similarly P4 must be opposite P1 when the sphere is halved by P2 and P3. And opposite P2 when the hemispheres are defined by P1 and P3. The probability of two random points being on opposite hemispheres is 1/2, so the combined probability of the point P4 simultaneously being on these three distinct hemispheres is 1/2 * 1/2 * 1/2 = 1/8.

Jonn Jonsen - 3 years, 2 months ago

Log in to reply

Thanks a lot for correcting me. Thought haven't been activated that Day on explaining my answer!

A I - 3 years, 2 months ago

Fixing one point on a sphere of course defines a distinct hemisphere, namely by the great circle of which each point has constant distance to that point. The problem with AI's reasoning is a different one (although it leads to the correct solution :-) ): You can easily construct a tetrahedron with P1...P3 on the distinct hemisphere defined by P1 and P4 on the other side.

Kramers Kronig - 3 years, 1 month ago
Amil Dravid
Apr 2, 2018

This is a Putnam problem.

2 Helpful 0 Interesting 0 Brilliant 0 Confused
Ariijit Dey
Apr 3, 2018

Well, I too viewed the video before and came to know about this beautiful solution...

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...