Spheres on a cone
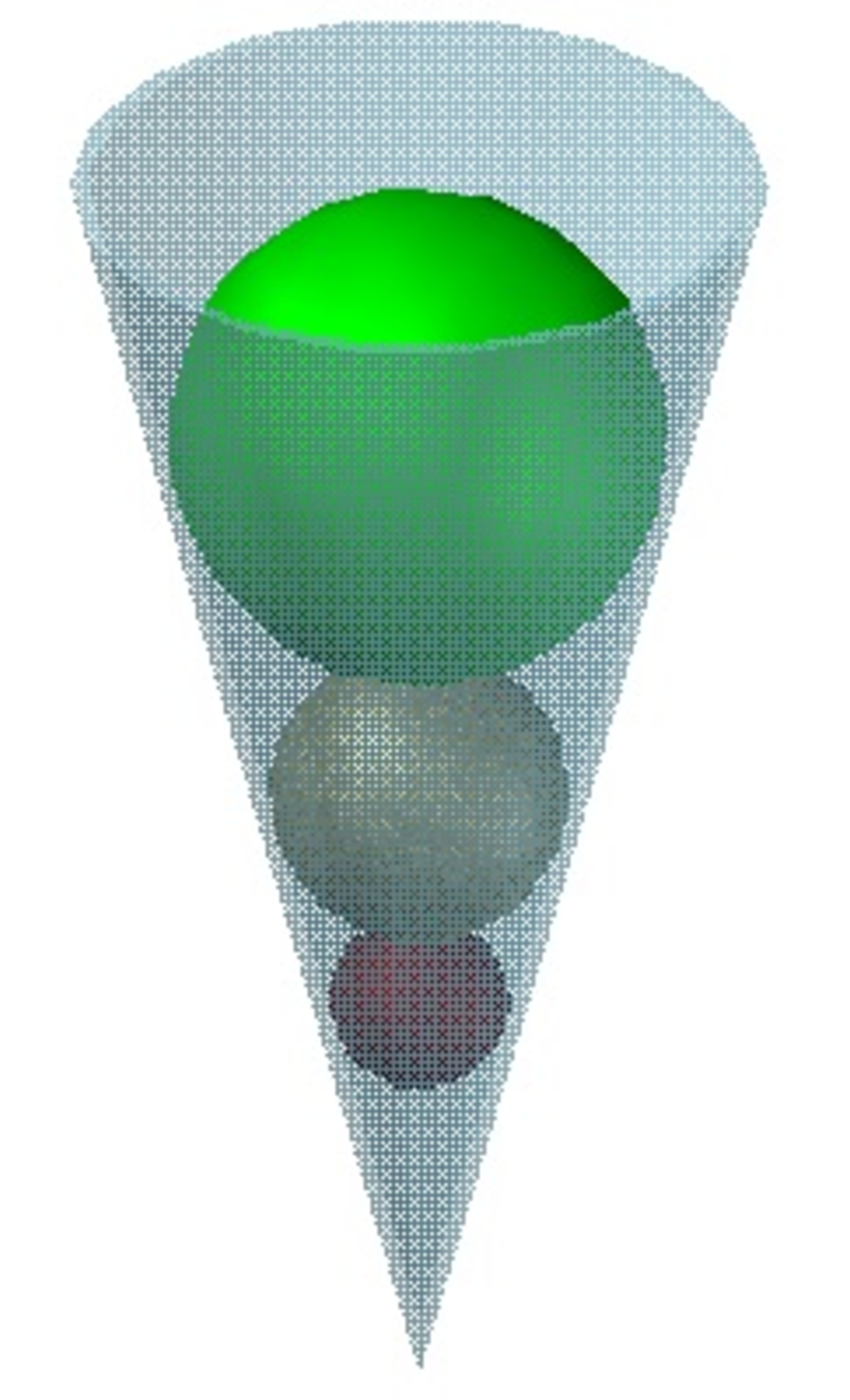Three spherical balls are placed inside an inverted right circular cone such that each ball is in contact with the cone and the next ball. If the radii of the balls are 16, x, and 5.76 (in decreasing order), respectively, what is the ratio of the volume of the largest ball to the volume of the ball at the middle?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Using similar triangles, we have
1 6 + x 1 6 − x = x + 5 . 7 6 x − 5 . 7 6
Cross-multiplying and simplifying, we get
( 1 6 − x ) ( x + 5 . 7 6 ) = ( 1 6 + x ) ( x − 5 . 7 6 )
1 6 x + 9 2 . 1 6 − x 2 − 5 . 7 6 x = 1 6 x − 9 2 . 1 6 + x 2 − 5 . 7 6 x
x 2 = 9 2 . 1 6
x = 9 . 6
The ratio of the volumes is 9 . 6 3 1 6 3 = 2 7 1 2 5