Spheres snugly fitted into a cube
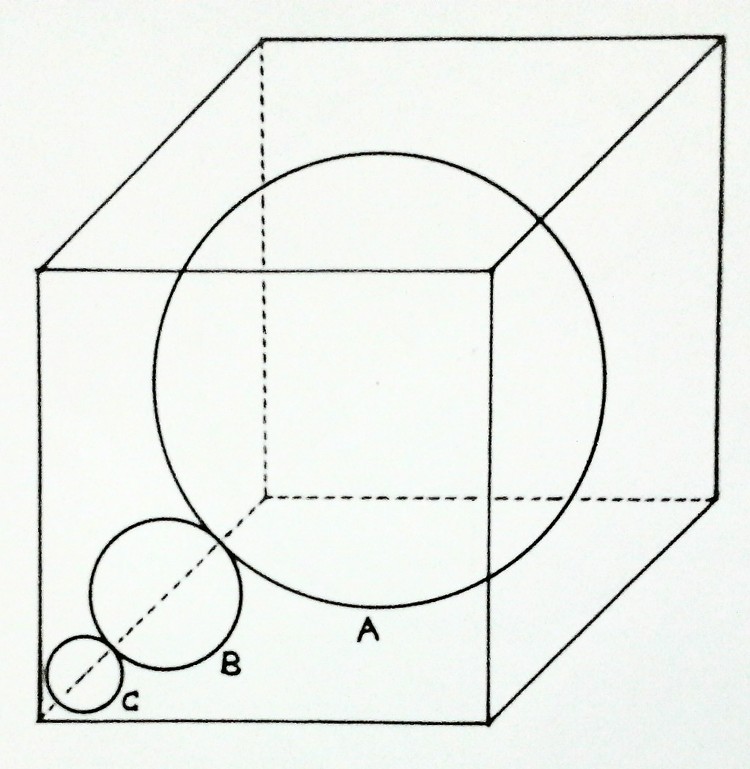 A larger sphere A, having a radius R, is snugly fitted in a cube (i.e. sphere A touches all six faces of the cube). Further, a small sphere B is snugly fitted in the corner of cube (i.e. sphere B touches sphere A & three orthogonal faces meeting at the same vertex). Further, a smaller sphere C, having a radius r, is snugly fitted in the same corner of the cube (i.e. sphere C touches sphere B & three orthogonal faces meeting at the same vertex). Find out ratio of the radius R (of larger sphere A) to the radius r (of smaller sphere C)?
A larger sphere A, having a radius R, is snugly fitted in a cube (i.e. sphere A touches all six faces of the cube). Further, a small sphere B is snugly fitted in the corner of cube (i.e. sphere B touches sphere A & three orthogonal faces meeting at the same vertex). Further, a smaller sphere C, having a radius r, is snugly fitted in the same corner of the cube (i.e. sphere C touches sphere B & three orthogonal faces meeting at the same vertex). Find out ratio of the radius R (of larger sphere A) to the radius r (of smaller sphere C)?
Details: None of the spheres touches any of 12 edges of the cube
The answer is 13.92820323.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Elegant! 2D to 3D was a great insight! So successive sphere radii are not only in geometric progression in space, but they are also doing a sequence in space of higher and higher dimensions! Thank you for noticing the typo. I corrected it.
Let R , C , S = Radius, distance of center and distance of sphere from the cube vertex
For any sphere C = 3 R
C B + R B = S A which gives R B = R A 3 + 1 3 − 1
Similarly, R C = R B 3 + 1 3 − 1 = R A 3 + 1 3 − 1 × 3 + 1 3 − 1
Hence, R C R A = ( 3 − 1 3 + 1 ) 2 = 1 3 . 9 2 8 2
@Harish Chandra Rajpoot @Niranjan Khanderia
Thank you for the solution. A nice one. +1). I am posting just an other angle.
Typo. Last line R C R A
In general, the radius r n of nth sphere is given as
r n = R ( 2 − 3 ) n − 1
hence, for third sphere r 3 = R ( 2 − 3 ) 2
r 3 R = ( 2 − 3 ) 2 1 ≈ 1 3 . 9 2 8 2
If it is a 2D problem,
A circle is tangent to the two adjacent sides of a square. Its center will be on the diagonal from the corner. It needs a length of
( 2 + 1 ) ∗ R from the corner. However it spares a legth of ( 2 − 1 ) ∗ R from the corner, for other circles. This is used by a smaller circle radius r, as ( 2 + 1 ) ∗ r .
That is ( 2 − 1 ) ∗ R = ( 2 + 1 ) ∗ r . ⟹ r R = 2 − 1 2 + 1 .
If there are n smaller and smaller circles, the ratio of original to the n-th circle will be .... r R = ( 2 − 1 2 + 1 ) n .
If it is 3D with sheres in a cube. 2 i s r e p l a c e d b y 3 . , since the distance of centers of the circles from the corner is now
from 2 R t o 3 R . S o a n s w e r t o o u r p r o b l e m i s { 3 − 1 3 + 1 } 2 = 1 3 . 9 2 8 2 0 .