Spheres within another sphere, how many more spheres?

This problem's question: **How many more spheres can be added?"

There are additional conditions and definitions. A sphere is the boundary of a closed ball. There are two spheres within the larger sphere. The sum of the radii of the two interior spheres does not have to equal the radius of the exterior sphere. All of these spheres have positive, finite radii and are mutually tangent (in contact). The added spheres must be tangent to all of the original three spheres and except for the first added sphere, must be tangent to at least one of the added spheres. Tangency is the only form of contact permitted by any of the spheres, original or added. Intrusion into the interior of another sphere is not permitted.

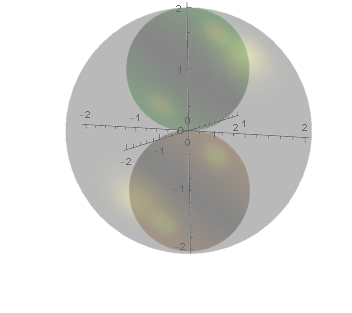
This is a permissible nesting of the original spheres.