Sphylinder
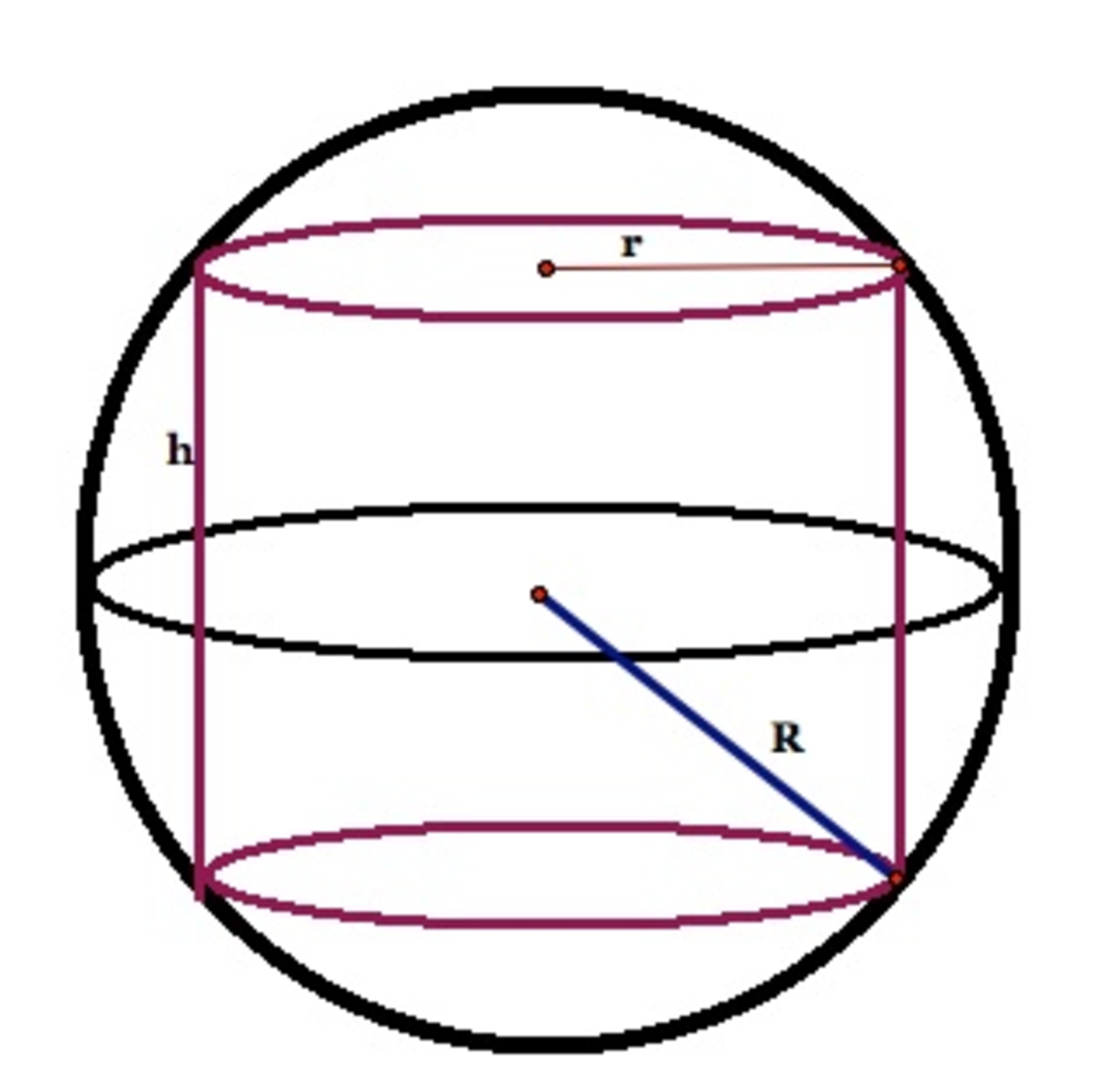
Consider a sphere of radius R , what is the maximum volume of a cylinder that can fit inside the sphere?
Image credit: The University of Georgia
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Thank You for posting a solution to my problem !!! cheers
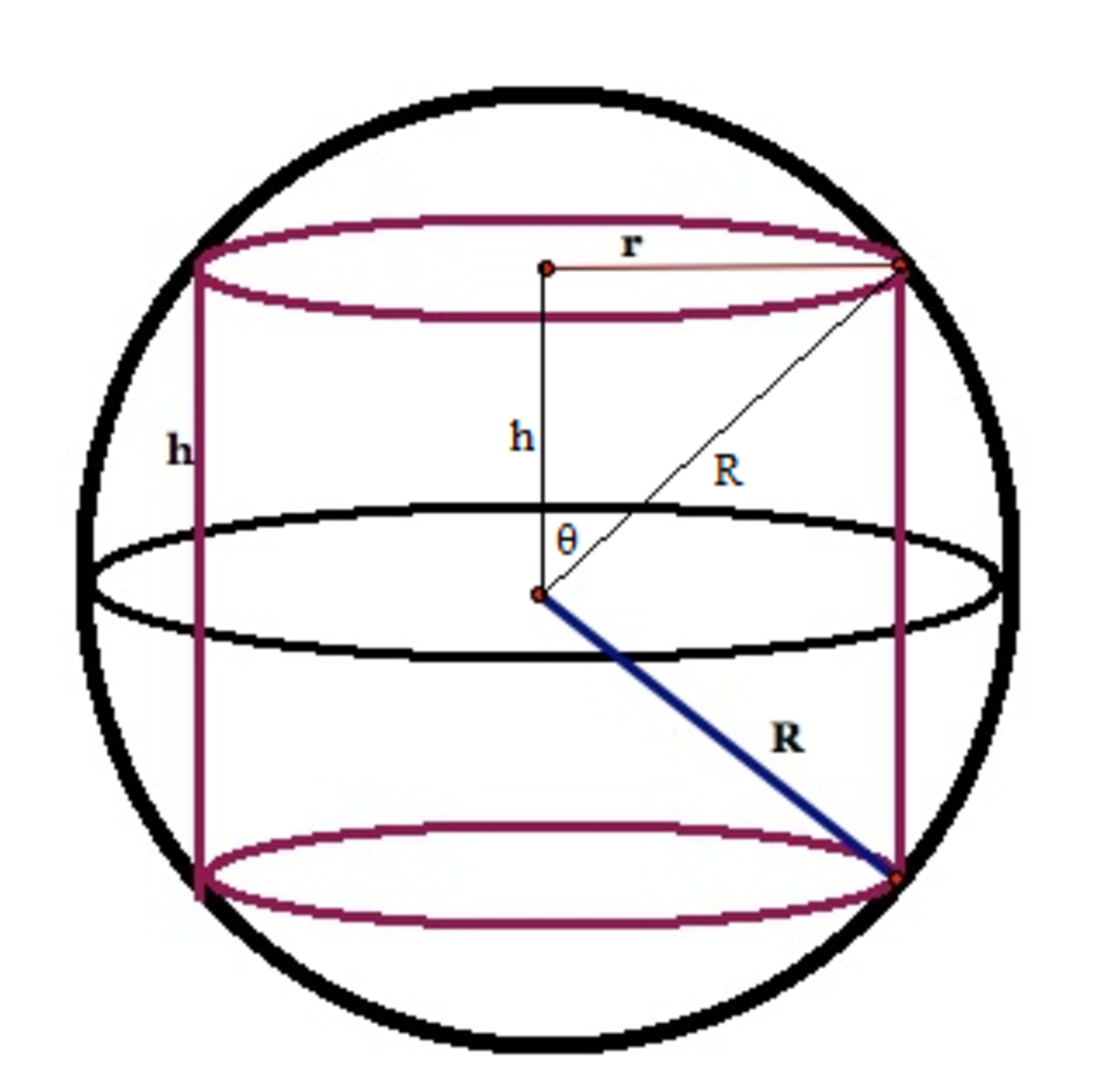
Let the base radius and height of the cylinder fit in the sphere be r and h respectively. If the polar angle between the zenith and R is θ , then we have r = R sin θ and 2 h = R cos θ . The volume V of the cylinder is given by:
V ⟹ d θ d V 2 sin θ ⟹ sin θ d θ 2 d 2 V = π r 2 h = 2 π R 3 sin 2 θ cos θ = 2 π R 3 ( 2 sin θ cos 2 θ − sin 3 θ ) = 2 π R 3 ( 2 sin θ − 3 sin 3 θ ) = 3 sin 3 θ = 3 2 = 2 π R 3 ( 2 cos θ − 9 sin 2 θ cos θ ) Note that cos 2 θ = 1 − sin 2 θ Equating d θ d V = 0 Note that sin θ = 0 gives minimum V ⟹ cos θ = 3 1 , tan θ = 2
⟹ d θ 2 d 2 V ∣ ∣ ∣ ∣ θ = tan − 1 2 = 2 π R 3 ( 3 2 − 3 2 ) < 0
This means that V is maximum when θ = tan − 1 2 and V max = 2 π R 3 × 3 2 × 3 1 = 3 3 4 π R 3 .
Let R be the radius of the sphere, h be the height of the cylinder and r be the radius of the cylinder. By the Pythagorean theorem, the radius of the cylinder is given by
r 2 = R 2 − ( 2 h ) 2 = R 2 − 4 h 2
The volume of the cylinder is hence
V = π r 2 h = π ( R 2 − 4 h 2 ) h = π ( R 2 h − 4 h 3 )
Differentiating with respect to h and equating to 0 to find extrema gives
d h d V = π ( R 2 − 4 1 × 3 h 2 ) = π ( R 2 − 4 3 h 2 ) = 0
R 2 = 4 3 h 2
h 2 = 3 4 R 2
h = 3 4 R 2 = 3 2 R
Substituting, we get
V = π ( R 2 − 3 4 × 4 1 R 2 ) ( 3 2 R ) = 3 4 × 3 π R 3
Note: Do not forget the second derivative check.