A number theory problem by Karan Arora
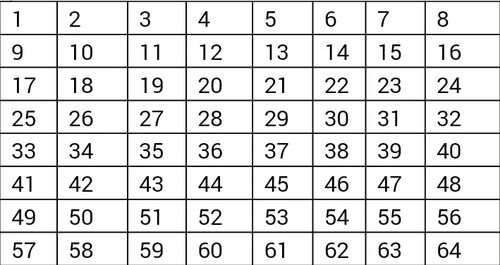Consider the 8x8 chessboard filled with numbers 1 to 64.If we choose 8 squares with the property that there is exactly one from each row & exactly one from each column, add up the numbers in the chosen squares, show that the sum obtained is 260.( you could give the proof in the solution)
The answer is 260.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
For the sake of exposition, lets write the given matrix as the sum of two matrices, a matrix A that contains the numbers 1, 2 ,..., 7, 8 in each row and a matrix B that contains the numbers 0, 8, 16, ... 48, 56 in each column. Let's add the chosen numbers in each of the matrices separately, and then add up the results. (To better understand what follows, the reader is invited to write down matrices A and B, at least in part; I'm too busy/lazy to do it myself.)
In matrix A, the number we pick in the first column will be 1 (since all the numbers in the first colum are 1). More generally, the chosen number in the c t h column will be c , and the sum will be 1 + 2 + . . . + 7 + 8 = 2 8 × 9 = 3 6 .
In matrix B, the number with pick in the first row will be 0, etc..... in the last row it will be 56. The sum will be 0 + 8 + 1 6 + . . . + 4 8 + 5 6 = 8 2 7 × 8 = 2 2 4 , for a grand total of 3 6 + 2 2 4 = 2 6 0 .