Spider on Artsy Lampshade
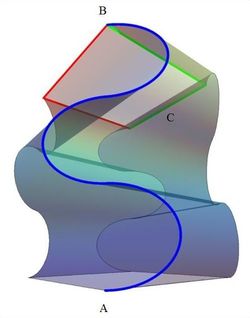 A spider at bottom corner
of an artistic lampshade spots Not-So-Brilli-the-Ant at top corner
. Not-So-Brilli-the-Ant panics and starts fleeing counter-clockwise at the top rim of the lampshade, along the green lines. The clever spider, moving twice as fast as Not-So-Brilli-the-Ant, takes the shortest distance on the surface of the lampshade to intercept point
, catches him, wraps him up in silk, and throws him into his food locker.
A spider at bottom corner
of an artistic lampshade spots Not-So-Brilli-the-Ant at top corner
. Not-So-Brilli-the-Ant panics and starts fleeing counter-clockwise at the top rim of the lampshade, along the green lines. The clever spider, moving twice as fast as Not-So-Brilli-the-Ant, takes the shortest distance on the surface of the lampshade to intercept point
, catches him, wraps him up in silk, and throws him into his food locker.
Here's another view of the lampshade from top down
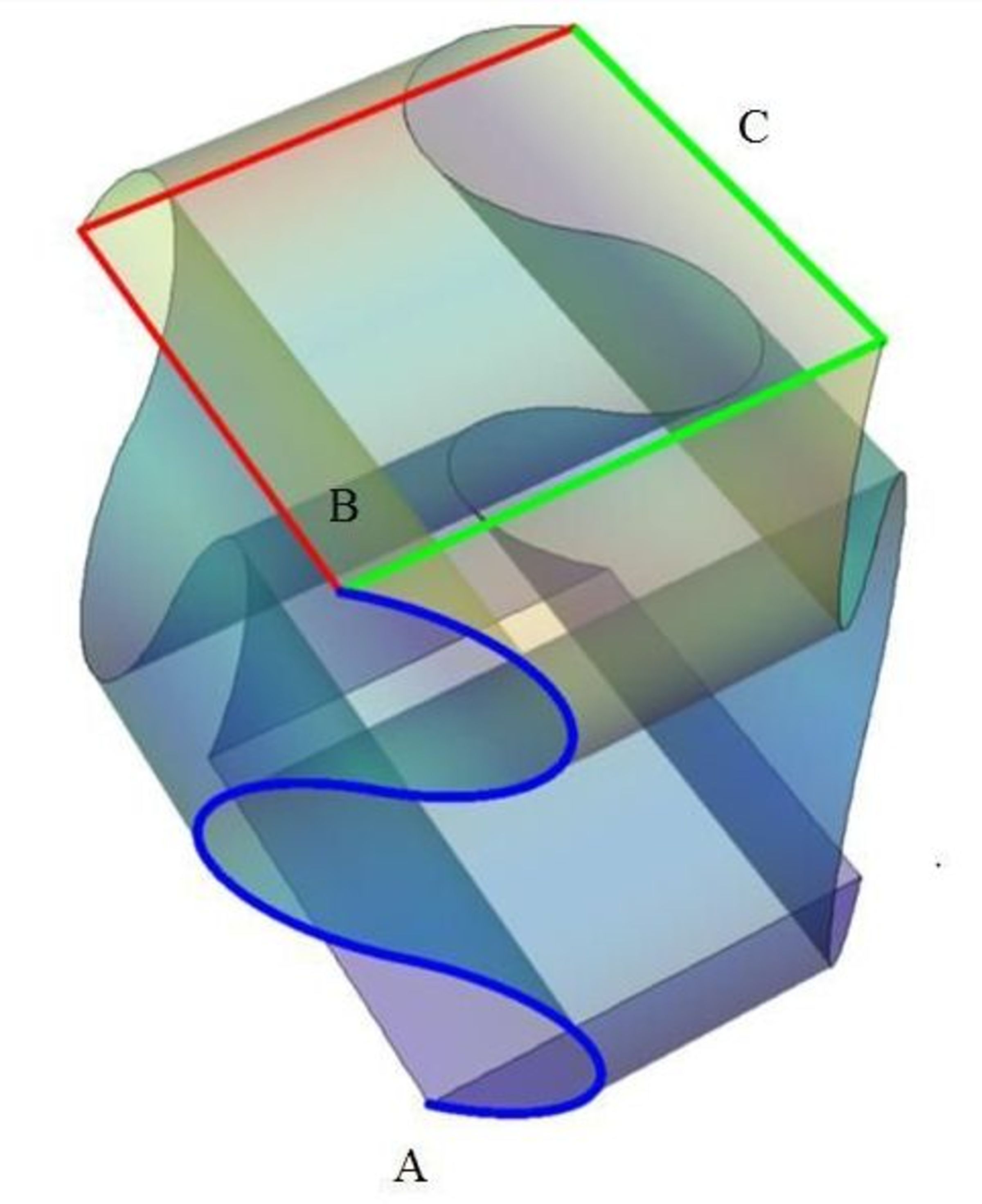
The top and bottom rims of the lampshade are perfect squares with sides. The lampshade is tall from bottom square rim to top square rim. The cross-section profile, orthgonal projections on or planes, as seen either from the right side or the left side of the spider, is made up of identical semi-circles stacked vertically. The lampshade is rotationally symmetric, i.e., it looks the same when rotated degrees about a central vertical axis.
How far did the spider travel from point
to point
?
If
is the path length on the surface in
, find
Okay, you don't need to use calculus for this.
The answer is 1088.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
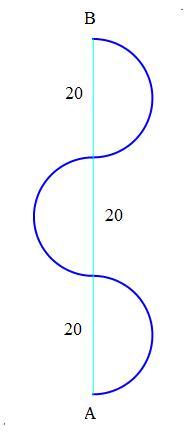
The exact path length is L = 2 0 3 π = 1 0 8 . 8 2 8 . . . , so that ⌊ 1 0 L ⌋ = 1 0 8 8 .
If the artsy lampshade was made out of paper, it can be laid out flat, with the creases showing as Sine functions. From the graphic below, one can see how the length of the path L = A C is worked out
![Artsy Lampshade Solution]
There's an interesting branch of origami that has curved creases, and many mathematical papers have been written on this subject. Technically, the 4 corners of this artsy lampshade are called "reflective folds".