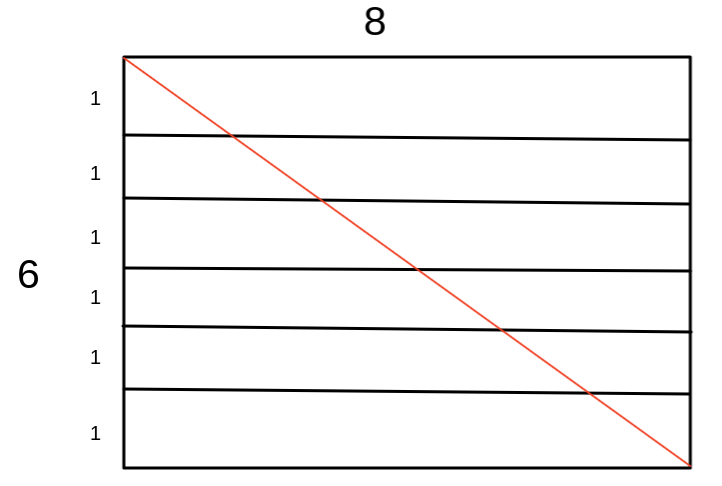
Spiky Problem!
Six straight, zigzagging lines are drawn inside an 8 × 1 rectangle. The drawing starts at the top left vertex and ends at the top right vertex.
What is the minimum possible sum of the lengths of these 6 segments?
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
13 solutions
I had that in mind! I just didn’t understand the question properly!
So elegant!
This is what I did. Reminds me of Heron's "Shortest Distance" problem.
This is brilliant!
This is elegant!
I was just about to give this solution. Too late!
Log in to reply
You Snooze - You Lose! lol
But in this case, take all of these positive comments above and below, and apply then to yourself also.
I love the way your brain, and Justin’s brain, work!
Never too late!
Great work.
Excellent solution - succinct and beautifully clear.
This is a pretty solution! I wondered how i can show that this is the minimal distance possible. Thanks for the way!
Log in to reply
If you mean prove the statement "the shortest distance between two points is a straight line", you could apply calculus to minimize arclength like here although it's definitely considered one of those known results that doesn't need re-proving every time.
Elegantly done.
what if there were 7 lines? would you still have connected the top left corner to the bottom right one, or, to the top right corner of the 7th box?
Log in to reply
If there were 7 lines, we would add another 1 by 8 box at the bottom. The line would still connect the top left corner to the bottom right one.
Ingenious Solution!!!! I Like the way you made the problem so easy
fantastic solution!
great way to visualize the solution
That's an awesome way to look at this.
Genius solution
Wow great solution
That is out of box thinking...
Wow this is why math is so interesting! You made it look so simple and yet that was not my approach.
How did you come about this solution? Is each box just alternated flipped sections where the line bounced from a wall?
Now you just valley and mountain fold the rectangle along the length and theres the minimum path. (Mind blown)
Covering space.
I love the way your brain, and Subin Manandhar’s brain works. I, like many others ‘felt’ that equal triangles in this case equaled the minimum distance, and from there calculated the correct answer. Unfortunately ‘feeling’ doesn’t count in mathematics. Your ‘proof’ is one that a child or uneducated adult could easily understand. I hope you are a mathematics teacher wherever you are. Thank you so much for sharing.
Nice creativity
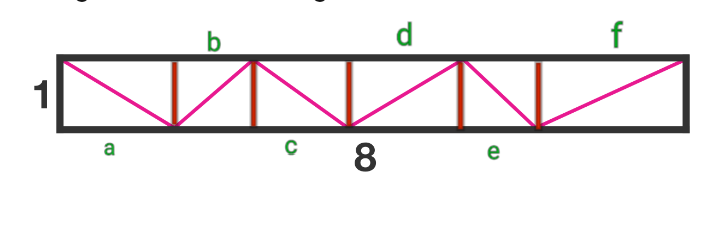 Let
l
1
,
l
2
,
⋯
,
l
6
be the length of hypotenuse of each right angles triangles (above).
Clearly
l
1
=
a
2
+
1
,
l
2
=
b
2
+
1
,
⋯
,
l
6
=
f
2
+
1
To minimize the sum of the length of the 6 segments we apply AM-GM inequality
l
1
+
l
2
+
⋯
+
l
6
≥
6
6
l
1
⋅
l
2
⋯
l
5
⋅
l
6
Equality occurs if
l
1
=
l
2
=
⋯
=
l
5
=
l
6
⟹
a
=
b
=
⋯
=
f
a
=
b
=
c
=
d
=
e
=
f
=
3
4
⟹
l
1
=
l
2
=
⋯
=
l
6
=
(
3
4
)
2
+
1
=
3
5
Hence,
l
1
+
l
2
+
⋯
+
l
6
≥
6
6
(
3
5
)
6
≥
1
0
Therefore, the minimum possible answer is
1
0
.
Let
l
1
,
l
2
,
⋯
,
l
6
be the length of hypotenuse of each right angles triangles (above).
Clearly
l
1
=
a
2
+
1
,
l
2
=
b
2
+
1
,
⋯
,
l
6
=
f
2
+
1
To minimize the sum of the length of the 6 segments we apply AM-GM inequality
l
1
+
l
2
+
⋯
+
l
6
≥
6
6
l
1
⋅
l
2
⋯
l
5
⋅
l
6
Equality occurs if
l
1
=
l
2
=
⋯
=
l
5
=
l
6
⟹
a
=
b
=
⋯
=
f
a
=
b
=
c
=
d
=
e
=
f
=
3
4
⟹
l
1
=
l
2
=
⋯
=
l
6
=
(
3
4
)
2
+
1
=
3
5
Hence,
l
1
+
l
2
+
⋯
+
l
6
≥
6
6
(
3
5
)
6
≥
1
0
Therefore, the minimum possible answer is
1
0
.
Wow. I love how you didn't just discard the zigzaged the shape but formalised how it should be redrawn. Beautiful solution.
The idea of using AM-GM is good. But there is one fundamental problem: The RHS of the AM-GM inequality is not a constant number. Considering a case in which not all 6 segments have the same length. Now LHS>RHS in your inequality. However, it is possible that this RHS now is far less than the RHS/LHS of the (in)equality you would obtain when all 6 segments are the same. And if the LHS now is only slightly larger than the RHS, this LHS could be indeed less than the LHS you get in your equality in the case that all 6 segments are the same!
Your use of AM-GM is incorrect. You showed that l 1 + l 2 + ⋯ + l 6 is minimized compared to 6 6 l 1 ⋅ l 2 ⋯ l 5 ⋅ l 6 when l 1 = l 2 = ⋯ = l 5 = l 6 . You did not show that l 1 + l 2 + ⋯ + l 6 is minimized when l 1 = l 2 = ⋯ = l 5 = l 6 .
Log in to reply
We can relate AM-GM with Jensen inequality which can shows l 1 + l 2 + l 3 + ⋯ + l 6 is minimized when l 6 = l 5 = ⋯ = l 2 = l 1 .
You using AM-GM correct but your solution nevertheless is wrong. The whole ideal to use AM-GM is to fix one side of the inequality to a fixed known quantitiy. In this case it would be a + b + c + d + e + f = 8 . When you have a vary RHS then it isn't a minimum. For example, x 2 + y 2 ≥ 2 ( x + y ) 2 but you can't say the RHS is the minimum. In fact it also greater than 2 x y .
Minimum possible distance is when they are equally spaced out. By dividing up, we see that one length is the hypotenuse of the triangle with other sides 3 4 & 1 making one of the line segments have length 3 5 and the total being 6 × 3 5 = 1 0
Your assertion that the minimum possible distance is when they are equally spaced out is correct, but you need to justify it.
We see that we must move a horizontal distance of 8 and a vertical distance 6×1=6. To optimize the distance, use pythagorean's theorem: sqrt (6^2+8^2)=10.
To gain the minimum length of the sum of the six lengths, make each length the same length (unlike in the diagram where each of the lines are differmet lengths). By this I mean divide up the points where each line touches the edge of the rectangle into equal distances apart. To do this do 6 8 , which is 3 4 . This gives you the base length of each of these small right angled triangles formed when making each length equal. By using simple Pythagoras you can calculate the length of one of these lines:
3 4 2 + 1 2 = 3 5
Because there are six lines all together, multiply this by six, which gives 10.
Can be solved by considering the path as the path followed by light and the sides as mirrors. Now Fermat principle (which can be easily proved) says the path is minimum for i=r. This makes all the triangles identical. and the length of each segment 5/3 and hence the total length 5/3 x 6 = 10
As the entire length has to be definitely and only be covered by 6 segments we can intuitively divide the box into 3 parts with two right-angled triangles each

-
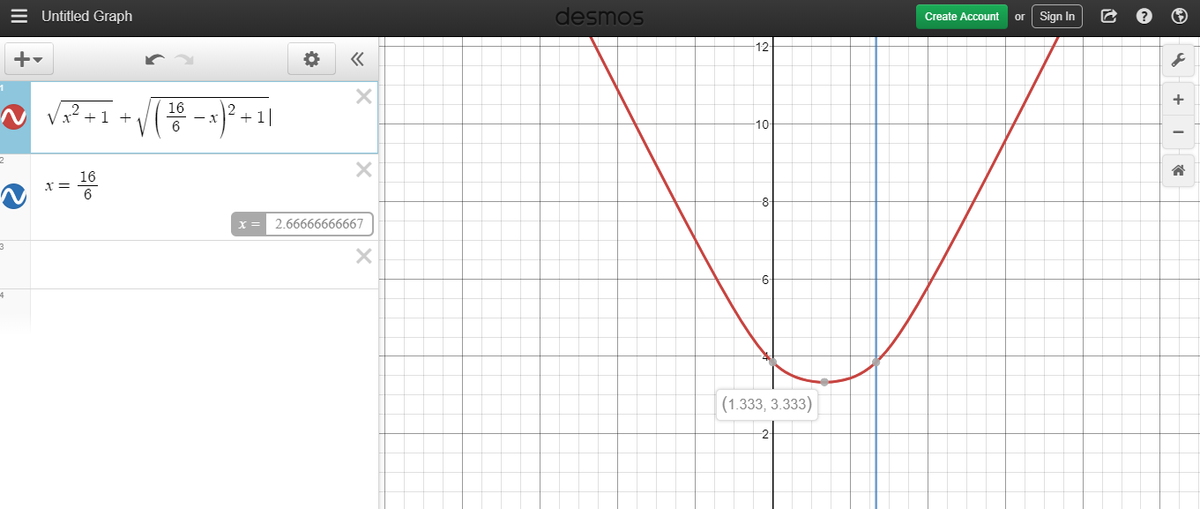
The cut off rectangle is in the dimension 2.667 * 1. We can make an equation for the sum of the two segments.
√((X^2)+1) + √(
3
8
-x)^2 + 1). The X is a variable and the length of the base of one of the triangles. (Can be any)
Through the graph below we find the best value of x to obtain the smallest total value is 1.33. The smallest total value is 3.33. When we multiply this by 3 we get 10
Let's think about this in terms of complex numbers.
Let the sides of length
8
and
1
be parallel to real and imaginary axis respectively.
Now, we can think of these segments as complex numbers, a k ± i , where k ∈ [ 1 , 6 ] are real and k = 1 ∑ 6 a k = 8
Now, length of the segment associated with a k is a k 2 + 1
However, the function x 2 + 1 happens to be a convex function meaning that according to Jensen's inequality, k = 1 ∑ 6 a k 2 + 1 ≥ 6 ( 6 1 k = 1 ∑ 6 a k ) 2 + 1 = 1 0
Equality is attained when all a k are equal meaning that the solution is 1 0
Using Fermat's principle( link text ),we can assume that there's a beam of light going though the rectangle with total reflection.Then there will be six congruent right triangles.We can get the answer by multiplying 3 5 and 6.
I disagree with the solution. Or I'm missing a criteria. If the first 5 lines are virtually vertical, their lengths are very nearly 1. The last line would then virtually cross the diagonal of the 1x8 rectangle (root 65... approx 8.06). This gives a total length approaching 13.06.
The problem is asking for the minimum total length. Since 1 0 < 1 3 . 0 6 , the total length given by other solutions is less than yours, and yours cannot be the minimum.
We can imagine the path of the lines as a beam of light, and we know that light always moves with the least action. We also know that the angle of incidence is equal to the angle of reflection for a light beam, so the reflected ray from every reflection is a mirrored version of the incident ray. Thus, all the lengths are identical to the first one, which traverses 8/6 units across and 1 units down, for a length of 1 + 6 8 2 . Because there are 6 identical segments, the total length is 6 1 + 6 8 2 = 6 2 + 8 2 = 1 0 0 = 1 0 .
WOW for a bunch of smart people you sure make this hard.
Pythagorean Triples
A Pythagorean triple is a right triangle where all the sides are integers. One of the most popular Pythagorean triples is the 3-4-5 right triangle. 3 and 4 are the lengths of the shorter sides, and 5 is the length of the hypotenuse, the longest side opposite the right angle.
If you run through the Pythagorean Theorem on this one, you can see that it checks out:
3^1 + 4^1.33337 = 5^1.66667
3 + 5.33335 =8.33335
8.33335= 8.33335
1.66667x6=10.00002
We may think of this problem as choosing 6 distances a i such that ∑ i = 1 6 a i = 8 . The length of each segment will then be a i 2 + 1 and the function we want to minimize is ∑ i = 1 6 a i 2 + 1 . Using lagrange multipliers, the condition for a extreme value is a i + 1 a i = λ . In other words, a i + 1 a i must remain invariant in our choice of distances. With this in mind let's examine the solutions of the equation
x 2 + 1 x = y 2 + 1 y .
We may rewrite it as x 2 ( y 2 + 1 ) = y 2 ( x 2 + 1 ) ⟹ ( y x ) 2 + x 2 = ( y x ) 2 + y 2 ⟹ x 2 = y 2 ⟹ ∣ x ∣ = ∣ y ∣ ⟹ x = y . The last equality only follows because we are working with distances which are positive. From this we conclude that a i = a j . Let's say that a i = x . Then ∑ i = 1 6 a i = 8 ⟹ 6 x = 8 ⟹ x = 3 4 .
Finally, i = 1 ∑ 6 a i 2 + 1 = 6 ( 3 4 ) 2 + 1 = 1 0
Relevant wiki: Length and Area Problem Solving
Make six copies of the 1 by 8 rectangles and place them next to each as shown below, so they make a 6 by 8 rectangle. The minimum distance from the top left vertex to the bottom right vertex is a straight line, and Pythagorean theorm says that this line is 10