Spiral Area
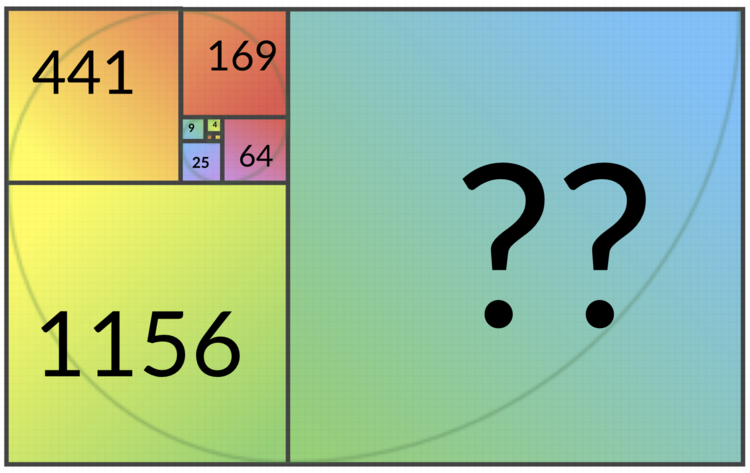 How many unit squares are there in the next square in this spiraling sequence?
How many unit squares are there in the next square in this spiraling sequence?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
In the figure, starting from the 3rd square in the spiral, notice that the side of any square is the sum of the sides of the previous 2 squares. For example, the 1 6 9 square (of side 1 3 ) can be expressed as 8 + 5 which is the sum of the previous 2 squares 6 4 and 2 5 .
Similarly, the side of the required square would be the side of the previous two squares. If you remember that the area of a square is a 2 where a is the side length, you can notice that the previous two squares have side lengths 3 4 ( 3 4 2 = 1 1 5 6 ) and 2 1 ( 2 1 2 = 4 4 1 ) . So the side would be 3 4 + 2 1 = 5 5 units. Reapplying the formula for area of a square, 5 5 2 = 3 0 2 5 .
First, you need to know that this is the Fibonacci Sequence:
1 , 1 , 2 , 3 , 5 … F n = F n − 1 + F n − 2
The only difference is each of a Fibonacci number has been squared:
1 , 1 , 4 , 9 , 2 5 … ( F n ) 2 = ( F n − 1 + F n − 2 ) 2
In this case, F n − 1 are 4 4 1 = 2 1 and F n − 2 are 1 1 5 6 = 3 4
Therefore, the final correct answer is ( 2 1 + 3 4 ) 2 = 5 5 2 = 3 0 2 5