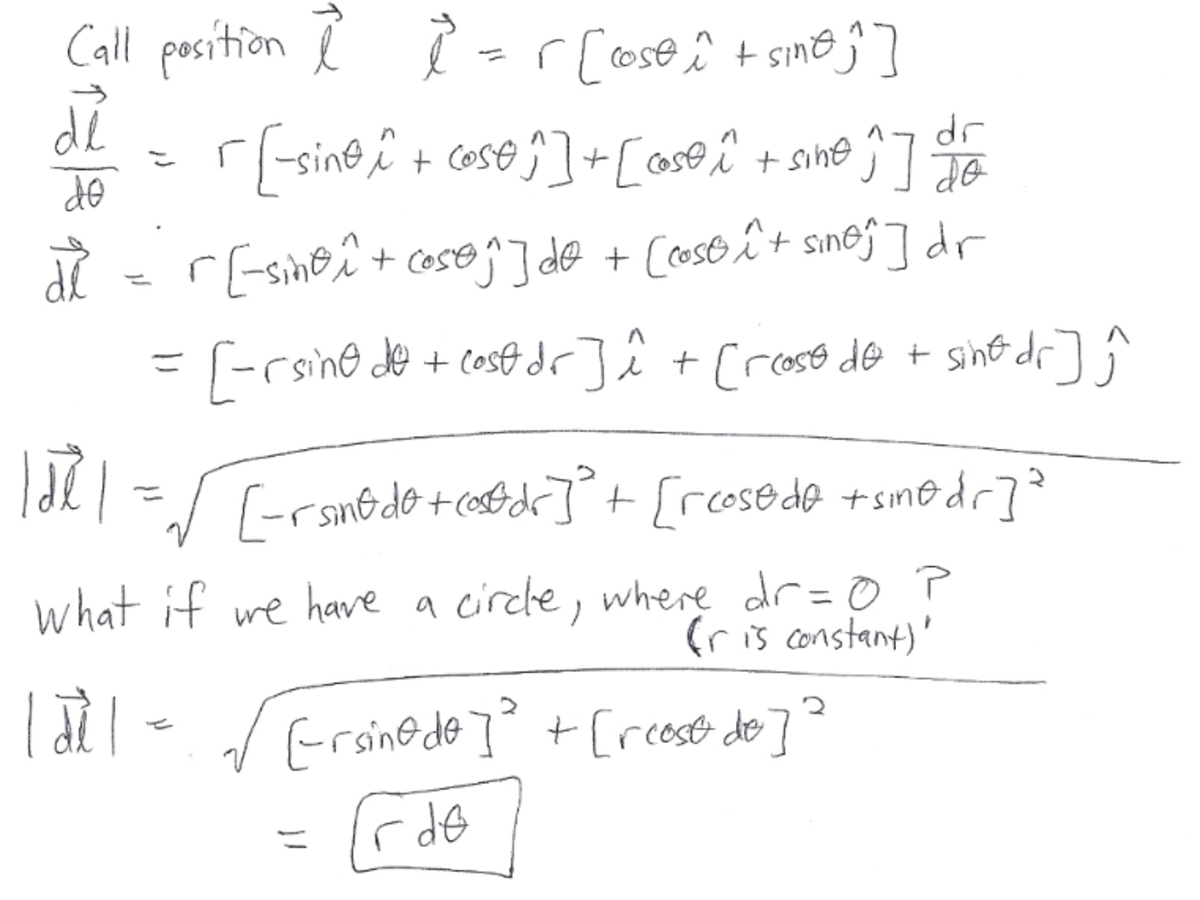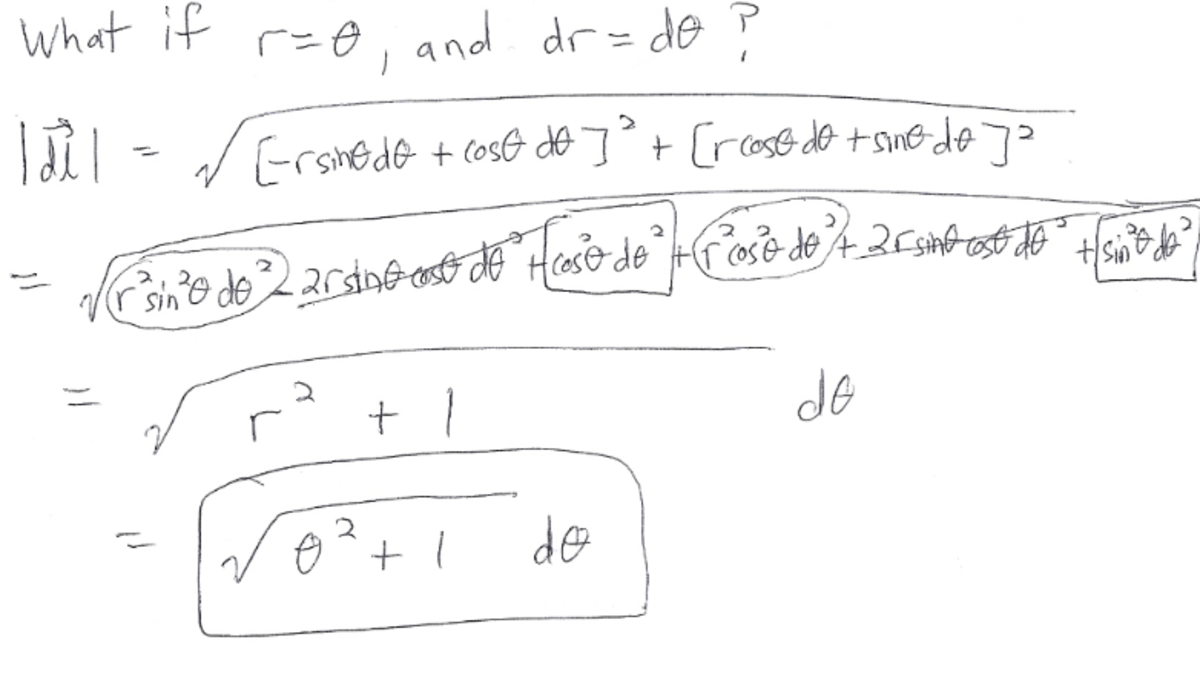Spiral Moment

Classical Mechanics Level 5

$x = \theta\cos(\theta)\hspace{1cm}y=\theta\sin(\theta)\hspace{1cm}0\leq\theta\leq4\sqrt{3}$

The spiral object described above exists in the $xy$ plane and has a linear mass density $(\sigma =\Large{\frac{1}{\theta}})$ .

Determine the object's moment of inertia with respect to an axis perpendicular to the $xy$ plane and passing through the point $(x,y) = (0,0)$ .

Details and Assumptions: All angles are in radians

The answer is 114.

2 solutions

Steven Chase
Sep 11, 2016

Here's another look at why the differential change in arc length is not simply equal to $r\, d\theta$ .

exactly same as me !! :)

A Former Brilliant Member - 4 years, 5 months ago

In polar form this equation is r=∅ So dL=rd∅-------for certain ∅ dm=Sigma*dl=d∅ Moment of inertia= integral r²dm =∅²d∅ from ∅ =0 to ∅=4√3 Which yields answer as 64√3 which is 110.85 Why are the two answers different?

Hrushikeshcoc Bodas - 4 years, 8 months ago

Hello. I believe the answer is that the differential arc length dL is only equal to r * d(theta) in certain cases, such as a circle. I have supplemented my original solution with some additional derivations confirming this. Please have a look at it.

Steven Chase - 4 years, 8 months ago

A Former Brilliant Member
Dec 24, 2016

the general form for moment of inertia is $\int dm*x^2$ where $x$ is a parameter , it is obvious from the quesion given that here it is $\theta$ and from here on..... find the arclength and it's small mass, integrate over the limits .. ..i have to say the limits are awesome as i was afraid how the answer will come out to be integer .... steven sir has alrady given pictorial solutions as i usually do ! nice one sir ..! the answer is 343/3-1/3 = 342/3 =114 answer !

Spiral Moment

The answer is 114.

2 solutions

0 pending reports